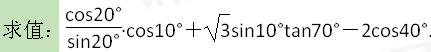如图,在梯形ABCD中,AB∥CD,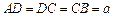 ,
,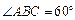 ,平面
,平面 平面
平面 ,四边形
,四边形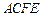 是矩形,
是矩形,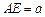 ,点
,点 在线段
在线段 上。
上。
(1)求证: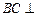 平面
平面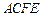 ;
;
(2)当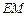 为何值时,
为何值时,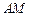 ∥平面
∥平面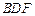 ?写出结论,并加以证明;
?写出结论,并加以证明;
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明。
(本小题满分12分)
已知函数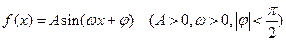 的图象与
的图象与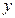 轴的交点为
轴的交点为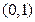 ,它在
,它在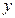 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为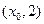 和
和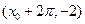 .
.
(1)求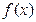 的解析式;
的解析式;
(2)若锐角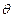 满足
满足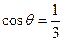 ,求
,求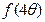 的值.
的值.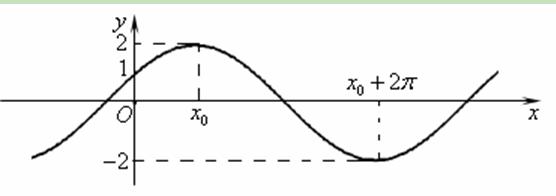
(本小题满分12分)
已知向量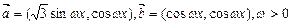 ,记函数
,记函数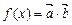 ,
,
若函数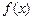 的最小正周期为
的最小正周期为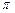 .
.
(1)求 的值;
的值;
(2)当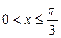 时,试求
时,试求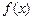 的值域;
的值域;
(3)求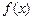 在
在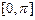 上的单调递增区间.
上的单调递增区间.
(本小题满分12分)在△ABC中, 若I是△ABC的内心, AI的延长线交BC于D, 则有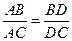 称之为三角形的内角平分线定理, 现已知AC=2, BC=3, AB=4, 且
称之为三角形的内角平分线定理, 现已知AC=2, BC=3, AB=4, 且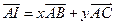 , 求实数
, 求实数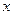 及
及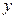 的值.
的值.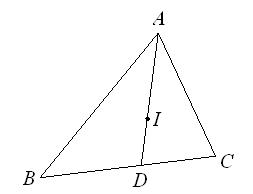
(本小题满分12分)
已知 ,
,
(1)求 和
和 的夹角;
的夹角;
(2)当 取何值时,
取何值时,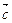 与
与 共线?
共线?
(3)当 取何值时,
取何值时,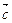 与
与 垂直?
垂直?
(本小题满分10分)