已知椭圆的中心在原点,焦点在x 轴上,离心率为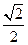 ,且椭圆经过圆C:
,且椭圆经过圆C: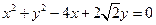 的圆心C。
的圆心C。
(1)求椭圆的方程;
(2)设直线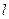 过椭圆的焦点且与圆C相切,求直线
过椭圆的焦点且与圆C相切,求直线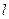 的方程。
的方程。
设定义在区间[x1,x2]上的函数y=f(x)的图象为C,M是C上的任意一点,O为坐标原点,设向
量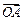 =
=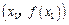 ,
,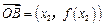 ,
,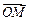 =(x,y),当实数λ满足x="λ" x1+(1-λ) x2时,记向
=(x,y),当实数λ满足x="λ" x1+(1-λ) x2时,记向
量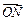 =λ
=λ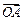 +(1-λ)
+(1-λ)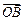 .定义“函数y=f(x)在区间[x1,x2]上可在标准k下线性近似”是指
.定义“函数y=f(x)在区间[x1,x2]上可在标准k下线性近似”是指
“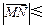 k恒成立”,其中k是一个确定的正数.
k恒成立”,其中k是一个确定的正数.
(1)设函数 f(x)=x2在区间[0,1]上可在标准k下线性近似,求k的取值范围;
(2)求证:函数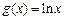 在区间
在区间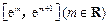 上可在标准k=
上可在标准k=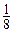 下线性近似.
下线性近似.
(参考数据:e =2.718,ln(e-1)=0.541)
=2.718,ln(e-1)=0.541)
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的
半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积; (2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
在平面直角坐标系 中,如图,已知椭圆E:
中,如图,已知椭圆E: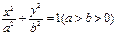 的左、右顶点分别为
的左、右顶点分别为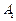 、
、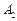 ,
,
上、下顶点分别为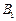 、
、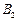 .设直线
.设直线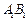 的倾斜角的正弦值为
的倾斜角的正弦值为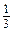 ,圆
,圆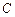 与以线段
与以线段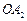 为直径的圆
为直径的圆
关于直线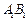 对称.
对称.
(1)求椭圆E的离心率;
(2)判断直线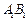 与圆
与圆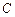 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆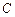 的面积为
的面积为 ,求圆
,求圆 的方程
的方程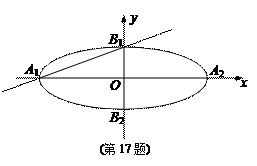
已知椭圆 的上、下顶点分别为
的上、下顶点分别为 是椭圆上两个不同的动点.
是椭圆上两个不同的动点.
(I)求直线 与
与 交点的轨迹C的方程;
交点的轨迹C的方程;
(Ⅱ)若过点F(0,2)的动直线z与曲线C交于A、B两点, 问在y轴上是否存在定点E,使得
问在y轴上是否存在定点E,使得 ?若存在,求出E点的坐标;若不存在,说明理由.
?若存在,求出E点的坐标;若不存在,说明理由.
已知函数 .
.
(I)若 ,求函数
,求函数 极值;
极值;
(II)设F(x)= ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求 的取值范围.
的取值范围.