 已知函数
已知函数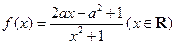 ,其中
,其中 .
.
(Ⅰ)当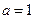 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值.
设函数
(1)将f(x)写成分段函数,在给定坐标系中作出函数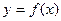 的图像;
的图像;
(2)解不等式f(x)>5,并求出函数y= f(x)的最小值。
⊙O1和⊙O2的极坐标方程分别为 。
。
(1)把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(2)求经过⊙O1,⊙O2交点的直线的直角坐标方程。
已知f(x)=2x3+ax2+bx+c在x=-1处取得极值8,又x=2时,f(x) 也取得极值。
(1)求a,b,c的值,写出f(x)的解析式;
(2)求f(x)的单调区间。
已知c>0.设命题P:函数y=cx在R上单调递减;Q: 函数 在
在 上恒为增函数.若P或Q为真,P且Q为假,求c的取值范围。
上恒为增函数.若P或Q为真,P且Q为假,求c的取值范围。
某桶装水经营部每天的房租,人员工资等固定成本为200元,每桶水的进价是5元。销售单价与日均销售的关系如下表所示
| 销售单价(元) |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 日均销售量(桶) |
480 |
440 |
400 |
360 |
320 |
280 |
240 |
设在进价基础上增加x元后,日均销售利润为y元。请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?