如图,椭圆 的离心率为
的离心率为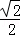 ,x轴被曲线
,x轴被曲线 截得的线段长等于C1的短轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于点D、E.
截得的线段长等于C1的短轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于点D、E.
(1)求C1、C2的方程;
(2)求证:MA⊥MB.
(3)记△MAB,△MDE的面积分别为S1、S2,若 ,求λ的取值范围.
,求λ的取值范围.
在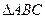 中,
中, 所对边分别为
所对边分别为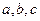 .已知
.已知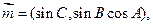
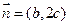 ,且
,且 .
.
(Ⅰ)求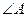 大小.
大小.
(Ⅱ)若 求
求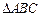 的面积
的面积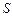 的大小.
的大小.
已知三点 、
、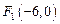 、
、 .
.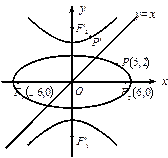
(Ⅰ)求以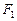 、
、 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点 、
、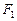 、
、 关于直线
关于直线 的对称点分别为
的对称点分别为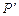 、
、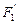 、
、 ,求以
,求以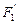 、
、 为焦点且过点
为焦点且过点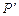 的双曲线的标准方程
的双曲线的标准方程
已知⊙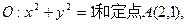 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足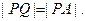
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程
随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数 ,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
已知圆C的半径为2,圆心在x轴的正半轴上,直线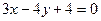 与圆C相切.
与圆C相切.
(I)求圆C的方程;
(II)过点Q(0,-3)的直线l与圆C交于不同的两点A 、B
、B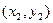 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积.