随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数 ,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
如图,在三棱锥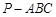 中,
中, 平面
平面 ,
,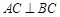 ,
, 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.
(1)证明: 平面
平面 ;
;
(2)求三棱锥 的体积;
的体积;
(3)在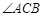 的平分线上确定一点
的平分线上确定一点 ,使得
,使得 平面
平面 ,并求此时
,并求此时 的长.
的长.
某班级共有60名学生,先用抽签法从中抽取部分学生调查他们的学习情况,若每位学生被抽到的概率为.
(1)求从中抽取的学生数;
(2)若抽查结果如下,先确定x,再完成频率分布直方图;
| 每周学习时间(小时) |
[0,10) |
[10,20) |
[20,30) |
[30,40 |
| 人数 |
2 |
4 |
x |
1 |
(3)估计该班学生每周学习时间的平均数(同一组中的数据用该组区间的中点值作代表).
已知函数f(x)= (其中A>0,
(其中A>0,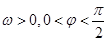 )的图象如图所示。
)的图象如图所示。
(1)求A,w及j的值;
(2)若tana=2,求 的值.
的值.
已知函数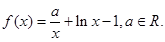
(1) 若曲线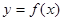 在
在 处的切线平行于直线
处的切线平行于直线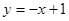 ,求函数
,求函数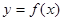 的单调区间;
的单调区间;
(2) 若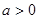 ,且对
,且对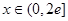 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知抛物线 y 2 =" –" x与直线 y =" k" ( x + 1 )相交于A、B两点, 点O是坐标原点.
(1) 求证: OA^OB;
(2) 当△OAB的面积等于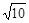 时, 求k的值.
时, 求k的值.