某班级共有60名学生,先用抽签法从中抽取部分学生调查他们的学习情况,若每位学生被抽到的概率为.
(1)求从中抽取的学生数;
(2)若抽查结果如下,先确定x,再完成频率分布直方图;
| 每周学习时间(小时) |
[0,10) |
[10,20) |
[20,30) |
[30,40 |
| 人数 |
2 |
4 |
x |
1 |
(3)估计该班学生每周学习时间的平均数(同一组中的数据用该组区间的中点值作代表).
(本小题满分14分)如图,正三棱柱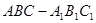 的侧棱长和底面边长均为
的侧棱长和底面边长均为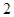 ,
, 是
是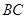 的中点.
的中点.
(Ⅰ)求证: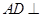 平面
平面 ;
;
(Ⅱ)求证: ∥平面
∥平面 ;
;
(Ⅲ)求三棱锥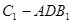 的体积.
的体积.
(本小题满分13分)某种零件按质量标准分为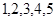 五个等级.现从一批该零件中随机抽取
五个等级.现从一批该零件中随机抽取 个,对其等级进行统计分析,得到频率分布表如下:
个,对其等级进行统计分析,得到频率分布表如下:
| 等级 |
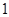 |
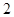 |
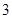 |
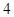 |
 |
| 频率 |
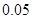 |
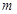 |
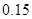 |
 |
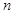 |
(Ⅰ)在抽取的 个零件中,等级为
个零件中,等级为 的恰有
的恰有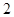 个,求
个,求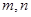 ;
;
(Ⅱ)在(Ⅰ)的条件下,从等级为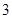 和
和 的所有零件中,任意抽取
的所有零件中,任意抽取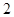 个,求抽取的
个,求抽取的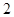 个零
个零
件等级恰好相同的概率.
(本小题满分13分)已知函数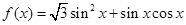 ,
, .
.
(Ⅰ)求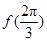 的值;
的值;
(Ⅱ)求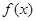 的最大值和最小值.
的最大值和最小值.
(本小题满分13分)已知数列 .如果数列
.如果数列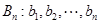 满足
满足 ,
, ,其中
,其中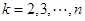 ,则称
,则称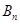 为
为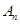 的“衍生数列”.
的“衍生数列”.
(Ⅰ)若数列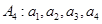 的“衍生数列”是
的“衍生数列”是 ,求
,求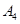 ;
;
(Ⅱ)若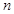 为偶数,且
为偶数,且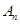 的“衍生数列”是
的“衍生数列”是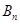 ,证明:
,证明: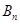 的“衍生数列”是
的“衍生数列”是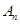 ;
;
(Ⅲ)若 为奇数,且
为奇数,且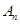 的“衍生数列”是
的“衍生数列”是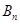 ,
,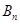 的“衍生数列”是
的“衍生数列”是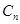 ,….依次将数列
,….依次将数列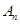 ,
,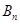 ,
,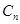 ,…的第
,…的第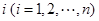 项取出,构成数列
项取出,构成数列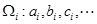 .证明:
.证明: 是等差数列.
是等差数列.
(本小题满分14分)已知函数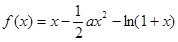 ,其中
,其中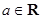 .
.
(Ⅰ)若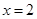 是
是 的极值点,求
的极值点,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若 在
在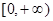 上的最大值是
上的最大值是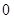 ,求
,求 的取值范围.
的取值范围.