如图梯形ABCD，AD∥BC,∠A=900，过点C作CE∥AB，AD=2BC，AB=BC,，现将梯形沿CE
折成直二面角D-EC-AB.
（1）求直线BD与平面ABCE所成角的正切值；
（2）设线段AB的中点为
，在直线DE上是否存在一点
，使得
∥面BCD？若存在，请指出点的位置，并证明你的结论；若不存在，请说明理由；
已知向量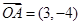
，
，
．
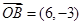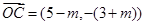（1）若点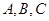
能构成三角形，求实数
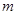应满足的条件；
（2）若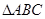
为直角三角形，且
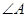为直角，求实数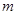的值．
求值：
（1）
+
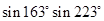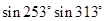
（2）
已知双曲线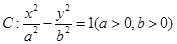
的两个焦点为
、
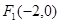点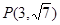
在双曲线C上．
(1)求双曲线C的方程；
(2)记O为坐标原点，过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F，若△OEF的面积为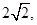
求直线l的方程．
某种产品的广告费用支出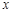
（万元）与销售额
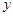（万元）之间有如下的对应数据：
|
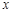2 |
4 |
5 |
6 |
8 |
|
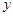30 |
40 |
60 |
50 |
70 |
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计广告费用为9万元时，销售收入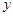的值．
参考公式：回归直线的方程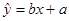
，其中
．
过点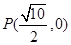
作倾斜角为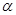
的直线与曲线
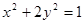交于点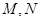
，
求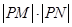
的最小值及相应的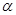的值。