（本小题满分14分）在直三棱柱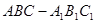
中，AC=4,CB=2,AA1=2，
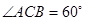，E、F分别是
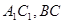的中点．（1）证明：平面
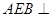平面
；
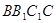（2）证明：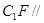
平面ABE；
（3）设P是BE的中点，求三棱锥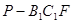
的体积．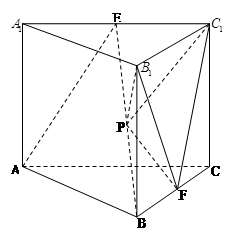
已知函数
满足
（1）求
的值并求出相应的
的解析式
（2）对于（1）中得到的函数，试判断是否存在
，使得
在[－1， 2]上值域为[－4，
]？若存在，求出；若不存在，请说明理由.
某商品定价为每件60元，不加收附加税时每年大约销售80万件，若政府征收附加税，每销售100元要征收
元(即税率为
)，因此每年销量将减少
万件.
(1)将政府每年对该商品征收的总税金
(万元)，表示成的函数，并指出这个函数的定义域；
(2)要使政府在此项经营中每年收取的税金不少于128万元，问税率应怎样确定？
已知函数
．
（1）求函数
的单调区间；
（2）函数的图象在
处切线的斜率为
若函数
在区间（1，3）上不是单调函数，求m的取值范围．
在计算“
”时，先改写第k项： 
由此得
……
相加，得
（1）类比上述方法，请你计算“
”的结果；
(2) 试用数学归纳法证明你得到的等式.
已知函数
图像上的点
处的切线方程为
.
（1）若函数
在
时有极值，求的表达式；
（2）函数在区间
上单调递增，求实数
的取值范围.