(本小题满分14分)
省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数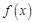 与时刻
与时刻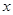 (时)的关系为
(时)的关系为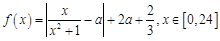 ,其中
,其中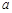 是与气象有关的参数,且
是与气象有关的参数,且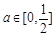 ,若用每天
,若用每天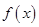 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作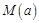 .
.
(1)令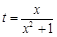 ,
,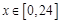 ,求t的取值范围;
,求t的取值范围;
(2)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性
污染指数是否超标?
为迎接建党90周年,某班开展了一次“党史知识竞赛”,竞赛分初赛和决赛两个阶段进行,在初赛后,把成绩(满分为100分,分数均为整数)进行统计,制成如图频率分布表:
(1)求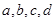 的值;
的值;
(2)决赛规则如下:为每位参加决赛的选手准备四道题目,选手对其依次作答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对一道,则获得二等奖.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同.设该同学决赛中答题个数为X,求X的分布列以及X的数学期望.
如图所示,在矩形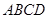 中,
中,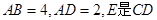 的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且 .
.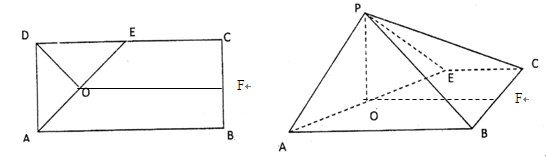
(1)求证:
(2)求二面角E-AP-B的余弦值.
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列 中的
中的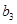 、
、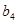 、
、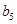 .
.
(1)求数列 的通项公式; (2)数列
的通项公式; (2)数列 的前n项和为
的前n项和为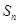 .
.
(本小题满分12分)
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点. 且PQ∥OA交OB于点Q.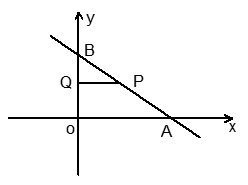
(1)若 和四边形
和四边形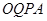 的面积满足
的面积满足 时,请你确定P点在AB上的位置,并求出线段PQ的长;
时,请你确定P点在AB上的位置,并求出线段PQ的长;
(2)在x轴上是否存在点M,使△MPQ为等腰直角三角形,若存在,求出点 与
与 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分12分)
如图,直三棱柱ABC—A1B1C1中,AC=BC=1,∠ACB=90°,AA1= ,D是A1B1中点.
,D是A1B1中点.
(1)求证:C1D⊥AB1;
(2)当点F在BB1上什么位置时,会使得AB1⊥平面C1DF?并证明你的结论.