已知函数f(x)= (其中A>0,
(其中A>0,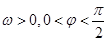 )的图象如图所示。
)的图象如图所示。
(1)求A,w及j的值;
(2)若tana=2,求 的值.
的值.
在△ 中,设内角
中,设内角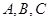 的对边分别为
的对边分别为 ,向量
,向量 向量
向量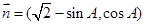 ,若
,若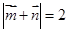
(1)求角 的大小;
的大小;
(2)若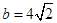 ,
, ,求△
,求△ 的面积。
的面积。
已知函数
(1)求函数 最小正周期;
最小正周期;
(2)若 ,求出该函数在
,求出该函数在 上的单调递增区间和最值。
上的单调递增区间和最值。
已知双曲线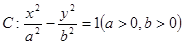 ,点
,点 在曲线
在曲线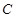 上,曲线
上,曲线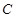 的离心率为
的离心率为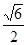 ,点
,点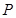 、
、 为曲线
为曲线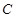 上易于点A的任意两点,
上易于点A的任意两点, 为坐标原点。
为坐标原点。
(1)求曲线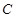 上方程;
上方程;
(2)若 为曲线
为曲线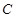 的焦点,求
的焦点,求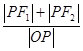 最大值;
最大值;
(3)若以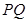 为直径的圆过点
为直径的圆过点 ,求证:直线
,求证:直线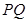 过定点,并求出定点坐标。
过定点,并求出定点坐标。
已知函数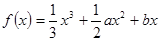 ,在区间
,在区间 内各有一个极值点。直线
内各有一个极值点。直线 是函数
是函数 在点
在点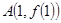 处的切线。
处的切线。
(1)求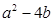 的取值范围。
的取值范围。
(2)当 在点
在点 处穿过函数
处穿过函数 的图像,求实数
的图像,求实数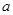 的值。
的值。
已知数列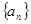 满足:
满足: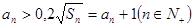 ,其中
,其中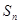 为
为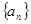 的前
的前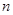 项和。
项和。
(1)求数列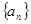 的通项公式;
的通项公式;
(2)若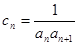 ,
,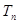 为
为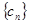 的前
的前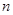 项和,且对任意
项和,且对任意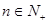 ,不等式
,不等式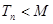 恒成立,求整数
恒成立,求整数 的最小值。
的最小值。