(本小题满分12分)已知集合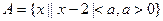 ,集合
,集合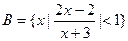 .
.
(Ⅰ)若 ,求
,求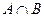 ;
;
(Ⅱ)若A B,求实数
B,求实数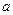 的取值范围.
的取值范围.
已知函数f(x)=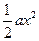 +
+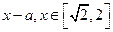 其中a为实数
其中a为实数
(1)求函数的最大值个
(2)若对于任意的非零实数a,不等式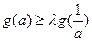 恒成立,求实数
恒成立,求实数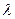 的取值范围。
的取值范围。
(本小题满分12分)
已知单调递增的等比数 列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(1)求数列{an}的通项公式;
(2)若b n=
n=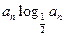 ,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
(本小题满分12分)
△ABC中,a,b,c分别是角A,B,C的对边,且有sin2C+ cos(A+B)=0.
cos(A+B)=0.
(1)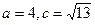 ,求△ABC的面积;
,求△ABC的面积;
(2)若 的值.
的值.
(本小题满分12分)
求与轴x轴相切,圆心在直线3x-y=0上,且被直线x-y=0截下的弦长2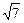 的圆的方程
的圆的方程