已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=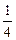 x2的焦点,离心率等于
x2的焦点,离心率等于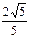 .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若 =λ1
=λ1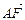 ,
,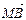 =λ2
=λ2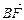 ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.
已知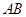 为半圆
为半圆 的直径,
的直径, ,
, 为半圆上一点,过点
为半圆上一点,过点 作半圆的切线
作半圆的切线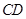 ,过点
,过点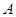 作
作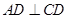 于
于 ,交圆于点
,交圆于点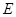 ,
,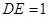 .
.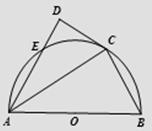
(Ⅰ)求证: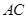 平分
平分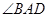 ;
;
(Ⅱ)求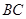 的长.
的长.
已知椭圆C的左、右焦点分别为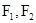 ,椭圆的离心率为
,椭圆的离心率为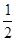 ,且椭圆C经过点
,且椭圆C经过点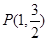 .
.
(1)求椭圆C的标准方程;
(2)若线段 是椭圆过点
是椭圆过点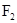 的弦,且
的弦,且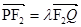 ,求
,求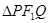 内切圆面积最大时实数
内切圆面积最大时实数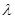 的值.
的值.
已知函数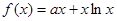 .
.
(1)当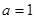 时,函数
时,函数 的图像在点
的图像在点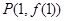 处的切线方程;
处的切线方程;
(2)当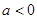 时,解不等式
时,解不等式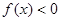 ;
;
(3)当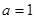 时,对
时,对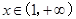 ,直线
,直线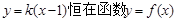 的图像下方.求整数
的图像下方.求整数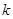 的最大值.
的最大值.
如图,正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求棱锥E-DFC的体积;
(3)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
 |
0.010 |
0.005 |
0.001 |
 |
6.635 |
7.879 |
10.828 |
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附: