某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元.根据市场调查,销售商一次订购量不会超过500件.
(1) 设一次订购量为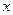 件,服装的实际出厂单价为
件,服装的实际出厂单价为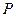 元,写出函数
元,写出函数 的表达式;
的表达式;
(2) 当销售商一次订购了450件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价-成本).
(本小题满分14分)
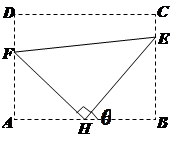
如图:某污水处理厂要在一个矩形污水处理池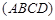 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 ,
,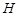 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口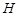 是
是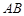 的中点,
的中点, 分别落在线段
分别落在线段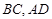 上。已知
上。已知 米,
米, 米,记
米,记 。
。
(Ⅰ)试将污水净化管道的长度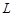 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
(Ⅱ)若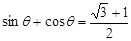 ,求此时管道的长度
,求此时管道的长度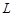 ;
;
(Ⅲ)问:当 取何值时,铺设管道的成本最低?并求出此时管道的长度。
取何值时,铺设管道的成本最低?并求出此时管道的长度。
(本小题满分14分)
已知函数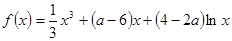 ,
,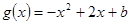
(Ⅰ)若 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)在(Ⅰ)的条件下,对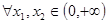 ,都有
,都有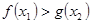 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅲ)若 在
在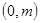 ,
, 上单调递增,在
上单调递增,在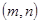 上单调递减,求实数
上单调递减,求实数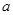 的取值范围。
的取值范围。
(本小题满分14分)
已知函数 ,
,
(Ⅰ)求函数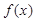 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)设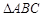 的内角
的内角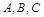 的对边分别
的对边分别 且
且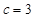 ,
,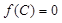 ,若
,若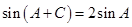 ,求
,求 的值.
的值.
(本小题满分12分)
在直角坐标系中,已知 ,
, ,
, 为坐标原点,
为坐标原点,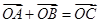 ,
,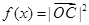 .
.
(Ⅰ)求 的对称中心的坐标及其在区间
的对称中心的坐标及其在区间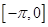 上的单调递减区间;
上的单调递减区间;
(Ⅱ)若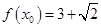 ,
,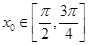 ,求
,求 的值。
的值。
(本小题满分12分)
已知集合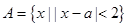 ,
, .
.
(Ⅰ)求集合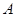 和集合
和集合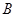 ;
;
(Ⅱ)若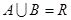 ,求
,求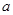 的取值范围。
的取值范围。