现在市面上有普通型汽车(以汽油为燃料)和电动型汽车两种。某品牌普通型汽车车价为12万元,第一年汽油的消费为6000元,随着汽油价格的不断上升,汽油的消费每年以20%的速度增长。其它费用(保险及维修费用等)第一年为5000元,以后每年递增2000元。而电动汽车由于节能环保,越来越受到社会认可。某品牌电动车在某市上市,车价为25万元,购买时一次性享受国家补贴价6万元和该市市政府补贴价4万元。电动汽车动力不靠燃油,而靠电池。电动车使用的普通锂电池平均使用寿命大约两年(也即两年需更换电池一次),电池价格为1万元,电动汽车的其它费用每年约为5000元。
求使用 年,普通型汽车的总耗资费
年,普通型汽车的总耗资费 (万元)的表达式
(万元)的表达式
(总耗资费=车价+汽油费+其它费用)
比较两种汽车各使用10年的总耗资费用
(参考数据:

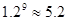
 )
)
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).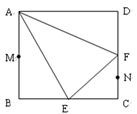
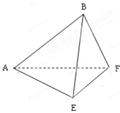
(Ⅰ)在三棱锥上标注出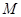 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ)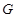 是线段
是线段 上一点,且
上一点,且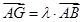 ,问是否存在点
,问是否存在点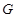 使得
使得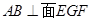 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
已知向量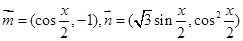 ,设函数
,设函数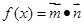 +
+
(1)若 ,f(x)=
,f(x)= ,求
,求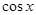 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是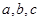 ,且满足
,且满足 ,求f(B)的取值范围.
,求f(B)的取值范围.
设数列 的前
的前 项和为
项和为 ,且
,且
 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)若数列 满足
满足 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
若a,b,c均为正数,且a+b+c=6,
 对任意x∈R恒成立,求m的取值范围.
对任意x∈R恒成立,求m的取值范围.