已知抛物线 与双曲线
与双曲线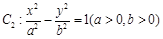 有公共焦点
有公共焦点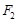 ,点
,点 是曲线
是曲线 在第一象限的交点,且
在第一象限的交点,且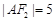 .
.
(Ⅰ)求双曲线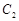 的方程;
的方程;
(Ⅱ)以双曲线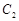 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆 与直线
与直线 相切,圆
相切,圆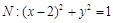 .过点
.过点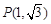 作互相垂直且分别与圆
作互相垂直且分别与圆 、圆
、圆 相交的直线
相交的直线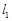 和
和 ,设
,设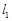 被圆
被圆 截得的弦长为
截得的弦长为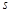 ,
, 被圆
被圆 截得的弦长为
截得的弦长为 ,问:
,问: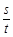 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
我市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a(a>0)件. 通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为x (0<x<1),那么月平均销售量减少的百分率为x2.记改进工艺后,旅游部门销售该纪念品的月平均利润是y(元)
(Ⅰ)写出y与x的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的销售价,使旅游部门销售该纪念品的月平均利润最大.
(本小题满分12分)
已知函数
(Ⅰ)求 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
已知函数 和函数
和函数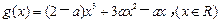
(Ⅰ)令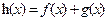 ,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
(Ⅱ)当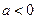 时,若
时,若 有极大值-7,求实数
有极大值-7,求实数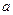 的值.
的值.
(本小题满分12分)
已知△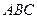 的内角
的内角 所对的边分别为
所对的边分别为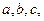 且
且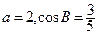 .
.
(Ⅰ)若 , 求
, 求 的值;
的值;
(Ⅱ)若△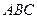 的面积
的面积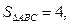 求
求 的值.
的值.
本小题满分12分)
设命题 :函数f(x)=x3-ax-1在区间
:函数f(x)=x3-ax-1在区间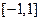 上单调递减;命题
上单调递减;命题 :函数
:函数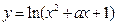 的定义域是
的定义域是 .如果命题
.如果命题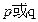 为真命题,
为真命题,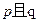 为假命题,求
为假命题,求 的取值范围.
的取值范围.