(本题12分)如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:
| 分组 |
人数 |
频率 |
| [39.5,49.5) |
a |
0.10 |
| [49.5,59.5) |
9 |
x |
| [59.5,69.5) |
b |
0.15 |
| [69.5,79.5) |
18 |
0.30 |
| [79.5,89.5) |
15 |
y |
| [89.5,99.5] |
3 |
0.05 |

(1)分别求出 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)估计这次环保知识竞赛平均分;
(3)若从所有参加环保知识竞赛的学生中随机抽取一人采访,抽到的学生成绩及格的概率有多大?
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量(吨) |
1 |
1.5 |
2 |
| 天数 |
10 |
25 |
15 |
若用样本估计总计,以上表频率为概率,且每天的销售量相互独立:
(1)求5天中该种商品恰好有2天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元,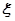 表示该种商品两天销售利润的和(单位:千元),求
表示该种商品两天销售利润的和(单位:千元),求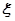 的分布列和数学期望.
的分布列和数学期望.
在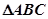 中,内角A, B, C的对边分别为
中,内角A, B, C的对边分别为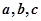 ,已知
,已知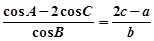 。
。
(1)求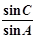 的值;
的值;
(2)若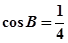 ,
,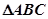 的周长为5, 求b的长度.
的周长为5, 求b的长度.
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用 的信息如下图。
的信息如下图。
(1)求 ;
;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
设数列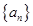 满足
满足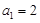 ,
, .
.
(1)求数列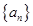 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列 的前
的前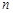 项和
项和 .
.
已知p:  , q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.
, q:x2-2x+1-m2≤0(m>0),若﹁p是﹁q的必要而不充分条件,求实数m的取值范围.