(本小题14分)已知点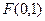 ,直线
,直线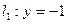 ,
,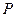 为平面上的动点,过点
为平面上的动点,过点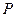 作直线
作直线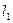 的垂线,垂足为点
的垂线,垂足为点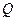 ,且
,且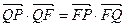 .
.
(1)求动点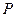 的轨迹
的轨迹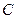 的方程;
的方程;
(2)轨迹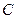 上是否存在一点
上是否存在一点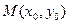 使得过
使得过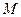 的切线
的切线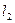 与直线
与直线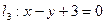 平行?若存在,求出
平行?若存在,求出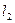 的方程,并求出它与
的方程,并求出它与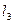 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
某公司经销某种产品,每件产品的成本为6元,预计当每件产品的售价为 元(
元(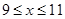 )时,一年的销售量为
)时,一年的销售量为 万件。
万件。
(1)求公司一年的利润y(万元)与每件产品的售价x的函数关系;
(2)当每件产品的售价为多少时,公司的一年的利润y最大,求出y最大值.
是否存在常数 使得
使得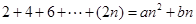 对一切
对一切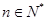 恒成立?若存在,求出
恒成立?若存在,求出 的值,并用数学归纳法证明;若不存在,说明理由.
的值,并用数学归纳法证明;若不存在,说明理由.
二阶矩阵 ;
;
(1)求点 在变换M作用下得到的点
在变换M作用下得到的点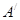 ;
;
(2)设直线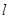 在变换M作用下得到了直线
在变换M作用下得到了直线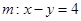 ,求
,求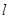 的方程.
的方程.
已知复数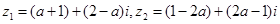 (其中
(其中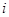 为虚数单位,
为虚数单位,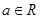 ),
),
若 为实数,
为实数,
(1)求实数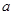 的值;
的值;
(2)求 .
.
已知椭圆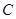 的中心在坐标原点,对称轴为坐标轴,焦点在
的中心在坐标原点,对称轴为坐标轴,焦点在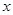 轴上,有一个顶点为
轴上,有一个顶点为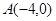 ,
,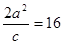 .
.
(1)求椭圆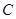 的方程;
的方程;
(2)过点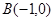 作直线
作直线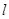 与椭圆
与椭圆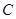 交于
交于 两点,线段
两点,线段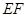 的中点为
的中点为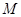 ,求直线
,求直线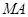 的斜率
的斜率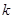 的取值范围.
的取值范围.