(文)如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问 与
与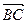 的夹角θ取何值时,
的夹角θ取何值时,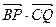 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。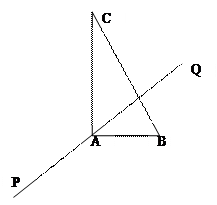

(理)如图9-6-6,矩形ABCD中,A B=1,BC=a,PA⊥平面ABCD
B=1,BC=a,PA⊥平面ABCD
(1)问BC边上是否存在Q点,使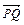 ⊥
⊥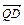 ,说明理由.
,说明理由.
(2)问当Q点惟一,且cos<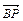 ,
,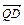 >=
>=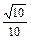 时,求点P的位置.
时,求点P的位置.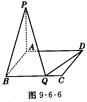
已知向量 =(1,
=(1, 1),向量
1),向量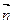 与向量
与向量 夹角为
夹角为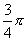 ,且
,且 =-1.
=-1.
(1)求向量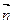 ;
;
(2)若向量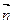 与向量
与向量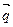 =(1,0)的夹角为
=(1,0)的夹角为 ,向量
,向量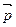 =
= ,其中A、C
,其中A、C
为△ABC的内角,且A、B、C依次成等差数列.求|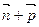 |的取值范围;
|的取值范围;
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
求以线段AB、AC为邻边的平行四边形两条对角线的长;设实数t满足
(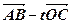 )·
)·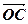 =0,求t的值。
=0,求t的值。
已知向量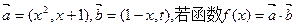 在区间(-1,
在区间(-1,
1)上是增函数,求t的取值范围.