已知圆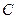 通过不同的三点
通过不同的三点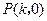 ,
, ,和
,和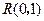 ,且该圆在点
,且该圆在点 处的切线的斜率等于1,求圆
处的切线的斜率等于1,求圆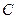 的方程.
的方程.
(本题满分10分)
设函数 ,
,
(Ⅰ)不等式 的解集为
的解集为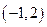 ,求
,求 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试求不等式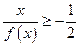 的解集.
的解集.
(本小题满分14分)
已知函数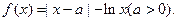
(Ⅰ)若 ,求
,求 的单调区间及
的单调区间及 的最小值;
的最小值;
(Ⅱ)若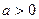 ,求
,求 的单调区间;
的单调区间;
(Ⅲ)证明:
本小题满分12分)
在下表中,每行上的数从左到右都成等比数列,并且所有公比都等于 ,每列上的数从上到下都成等差数列,正数
,每列上的数从上到下都成等差数列,正数 表示位于第
表示位于第 行第
行第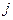 列的数,其中
列的数,其中
 |
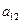 |
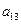 |
 |
… |
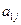 |
… |
 |
 |
 |
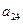 |
… |
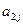 |
… |
 |
 |
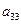 |
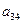 |
… |
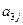 |
… |
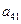 |
 |
 |
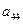 |
… |
 |
… |
| … |
… |
… |
… |
… |
… |
… |
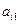 |
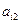 |
 |
 |
… |
 |
… |
| … |
… |
… |
… |
… |
… |
… |
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的计算公式;
的计算公式;
(Ⅲ)设数列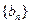 满足
满足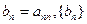 的前
的前 项和为
项和为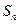 ,
,
试比较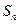 与
与 的大小,并说明理由。
的大小,并说明理由。
(本小题满分12分)
设函数
(Ⅰ)若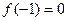 且对任意实数
且对任意实数 均有
均有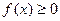 成立,求
成立,求 表达式;
表达式;
(Ⅱ)在(Ⅰ)的条件下,当 时,
时,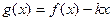 是单调函数,
是单调函数,
求实数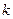 的取值范围;
的取值范围;
(Ⅲ)设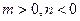 ,且
,且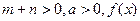 为偶函数,求证
为偶函数,求证
(本小题满分12分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是
,遇到红灯时停留的时间都是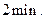
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停 留的总时间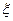 的分布列及期望
的分布列及期望