已知函数 .
.
(1)设 ,求
,求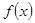 的值域;
的值域;
(2)在△ABC中,角 ,
, ,
,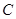 所对的边分别为
所对的边分别为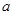 ,
,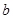 ,
,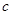 .已知c=1,
.已知c=1, ,且△ABC的面积为
,且△ABC的面积为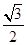 ,求边a和b的长.
,求边a和b的长.
设 ,函数
,函数 满足
满足 .
.
(Ⅰ)求 的单调递减区间;
的单调递减区间;
(Ⅱ)设锐角△ 的内角
的内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 , 求
, 求 的取值范围.
的取值范围.
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
| 学校 |
学校甲 |
学校乙 |
学校丙 |
学校丁 |
| 人数 |
 |
 |
 |
 |
该区篮球队经过奋力拼搏获得冠军,现要从中选出两名队员代表冠军队发言.
(Ⅰ)求这两名队员来自同一学校的概率;
(Ⅱ)设选出的两名队员中来自学校甲的人数为 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
已知函数 .
.
(Ⅰ)若 ,求函数
,求函数 的单调区间和极值;
的单调区间和极值;
(Ⅱ)设函数 图象上任意一点的切线
图象上任意一点的切线 的斜率为
的斜率为 ,当
,当 的最小值为1时,求此时切线
的最小值为1时,求此时切线 的方程.
的方程.
已知函数 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点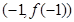 处的切线斜率为
处的切线斜率为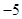 .
.
(1)求实数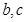 的值;
的值;
(2) 求函数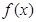 在区间
在区间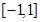 上的最小值;
上的最小值;
(Ⅲ)若函数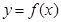 的图像上存在两点
的图像上存在两点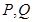 ,使得对于任意给定的正实数
,使得对于任意给定的正实数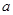 都满足
都满足 是以
是以 为直角顶点的直角三角形,且三角形斜边中点在
为直角顶点的直角三角形,且三角形斜边中点在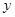 轴上,求点
轴上,求点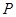 的横坐标的取值范围.
的横坐标的取值范围.
已知椭圆C: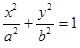
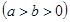 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(1)求椭圆C的方程;
(2)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的
对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.