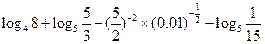

如图,长方体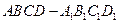 中,
中,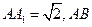
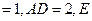 为
为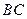 的中点
的中点
(1)求点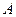 到面
到面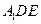 的距离;
的距离;
(2)设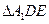 的重心为
的重心为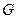 ,问是否存在实数
,问是否存在实数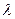 ,使
,使
得 且
且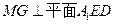 同时成立?若存
同时成立?若存
在,求出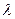 的值;若不存在,说明理由。
的值;若不存在,说明理由。
已知向量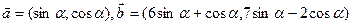 ,设函数
,设函数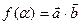 .
.
(Ⅰ)求函数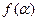 的最大值;
的最大值;
(Ⅱ)在锐角三角形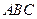 中,角
中,角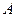 、
、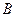 、
、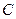 的对边分别为
的对边分别为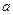 、
、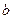 、
、 ,
,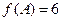 , 且
, 且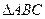 的面积为
的面积为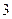 ,
,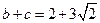
 ,求
,求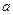 的值.
的值.
已知 两点在抛物线
两点在抛物线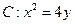 上,点
上,点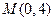 满足
满足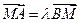
(I)求证: ;
;
(Ⅱ)设抛物线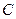 过
过 两点的切线交于点
两点的切线交于点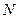
(1)求证:点N在一定直线上;
(2)设 ,求直线
,求直线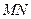 在
在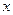 轴上截距的取值范围。
轴上截距的取值范围。
一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.
(1)求证: 平面ABD⊥平面ACD;
(2)求AD与BC所成的角;
(3)求二面角A—BD—C的大小.
设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=∠DBC=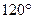 ,求:
,求:
(1)直线AD与平面BCD所成角的大小;
(2)异面直线AD与BC所成的角;
(3)二面角A—BD—C的大小. 