(本小题满分10分)根据函数单调性定义证明:函数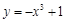 在
在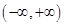 上是减函数.
上是减函数.
(本小题满分10分)已知集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求A∩B;
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
(本小题满分12分)已知函数 (
( )是偶函数.
)是偶函数.
(1)求k的值;
(2)若函数 的图象与直线
的图象与直线 没有交点,求
没有交点,求 的取值范围;
的取值范围;
(3)若函数 ,
, ,是否存在实数
,是否存在实数 使得
使得 最小值为
最小值为 ,若存在,求出
,若存在,求出 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由.
(本小题满分12分)设函数y= 是定义在
是定义在 上的减函数,并且满足
上的减函数,并且满足 =
= +
+ ,
,
(1)求 的值;
的值;
(2)若存在实数 ,使得
,使得 ,求
,求 的值;
的值;
(3)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品 (百台),其总成本为
(百台),其总成本为 (万元),其中固定成本为
(万元),其中固定成本为 万元,并且每生产1百台的生产成本为1万元(总成本
万元,并且每生产1百台的生产成本为1万元(总成本 固定成本+生产成本),销售收入
固定成本+生产成本),销售收入 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
(1)写出利润函数 的解析式(利润
的解析式(利润 销售收入—总成本);
销售收入—总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?