(本小题满分12分)某中学高二年级举行数学竞赛,共有800名学生参加.为了了解本次竞赛成绩,从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计。请你根据频率分布表,解答下列问题:
(1)填充下列频率分布表中的空格;
(2)估计众数、中位数和平均数;
(3)规定成绩不低于85分的同学能获奖,请估计在参加的800名学生中大概有多少名学生获奖?
| 分组(分数) |
频数 |
频率 |
| [60,70] |
① |
0.12 |
| [70,80] |
20 |
② |
| [80,90] |
③ |
0.24 |
| [90,100] |
④ |
⑤ |
| 合计 |
50 |
1 |
如图,椭圆C: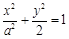 的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线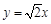 上一点P.
上一点P.
(1)求椭圆C及抛物线C1、C2的方程;
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M、N,已知点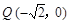 ,求
,求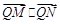 的最小值.
的最小值.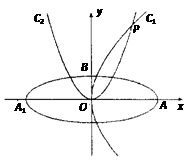
若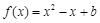 ,且
,且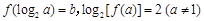 .
.
(1)求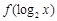 的最小值及对应的x值;
的最小值及对应的x值;
(2)若不等式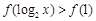 的解集记为A,不等式
的解集记为A,不等式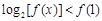 的解集记为B,求
的解集记为B,求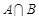 .
.
已知数列{bn}的前n项和 .数列{an}满足
.数列{an}满足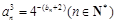 ,数列{cn}满足
,数列{cn}满足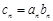 .
.
(1)求数列{an}和数列{bn}的通项公式;
(2)若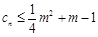 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
已知函数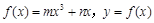 的图象在
的图象在 以点
以点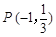 为切点的切线的倾斜角为
为切点的切线的倾斜角为 .
.
(1)求m、n的值;
(2)求函数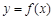 在
在 上的最大值和最小值.
上的最大值和最小值.
已知向量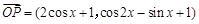 ,
, ,定义
,定义
(1)求出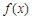 的解析式.当
的解析式.当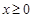 时,它可以表示一个振动量,请指出其振幅,相位及初相.
时,它可以表示一个振动量,请指出其振幅,相位及初相.
(2)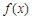 的图像可由
的图像可由 的图像怎样变化得到?
的图像怎样变化得到?
(3)设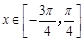 时
时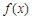 的反函数为
的反函数为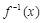 ,求
,求 的值.
的值.