(本小题满分12分)
甲、乙二名射击运动员参加今年深圳举行的第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):
| 甲 |
5 |
6 |
9 |
10 |
| 乙 |
6 |
7 |
8 |
9 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.
(本小题满分12分)斜三棱柱 中,侧面
中,侧面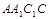
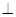 底面ABC,侧面
底面ABC,侧面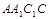 是菱形,
是菱形,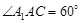 ,
,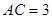 ,
,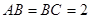 ,E、F分别是
,E、F分别是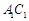 ,AB的中点.
,AB的中点.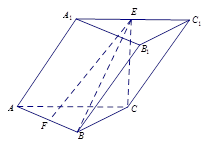
(1)求证:EF∥平面 ;
;
(2)求证:CE⊥面ABC.
(3)求四棱锥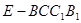 的体积.
的体积.
(本小题满分12分) 设函数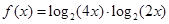 ,
,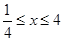 ,
,
(1)若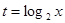 ,求
,求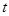 取值范围;
取值范围;
(2)求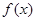 的最值,并给出最值时对应的x的值。
的最值,并给出最值时对应的x的值。
(本小题满分12分)如图,在四棱锥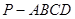 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点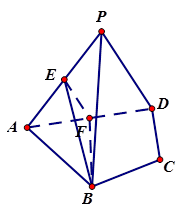
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD
(本小题满分12分)已知两直线l1:x+my+6=0 l2:(m-2)x+3my+2m=0
当m为何值时,l1与l2:
(1)平行;
(2)垂直;
(本小题满分10分) 已知P(3,2),一直线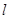 过点P,
过点P,
①若直线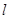 在两坐标轴上截距之和为12,求直线
在两坐标轴上截距之和为12,求直线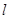 的方程;
的方程;
②若直线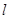 与x、y轴正半轴交于A、B两点,当
与x、y轴正半轴交于A、B两点,当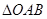 面积为12时求直线
面积为12时求直线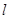 的方程.
的方程.