设数列{an}的前n项和为Sn=2n+1-2,{bn }是公差不为0的等差数列,其中b2、b4、b9依次成等比数列,且a2=b2
(1)求数列{an }和{bn}的通项公式: (2)设cn= ,求数列{cn)的前n项和Tn
,求数列{cn)的前n项和Tn
把长为10cm的细铁丝截成两段,各自围成一个正方形,求这两个正方形面积之和的最小值。
已知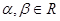 且
且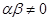 ,数列
,数列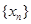 满足
满足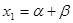 ,
,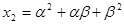 ,
,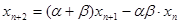 (
(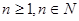 ),令
),令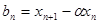 ,
,
⑴求证: 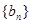 是等比数列;
是等比数列;
⑵求数列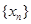 的通项公式;
的通项公式;
⑶若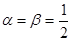 ,求
,求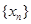 的前
的前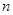 项和
项和 .
.
某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q亿元),它们与投资额t(亿元)的关系有经验公式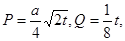 其中
其中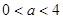 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
(1)求y关于x的解析式,
(2)怎样投资才能使总利润最大,最大值为多少?.
如图所示,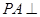 平面
平面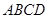 ,四边形
,四边形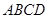 是矩形,
是矩形,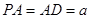 ,M,N分别是AB,PC的中点,
,M,N分别是AB,PC的中点,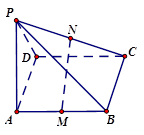
(1)求平面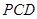 和平面
和平面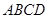 所成二面角的大小,
所成二面角的大小,
(2)求证: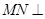 平面
平面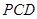
(3)当 的长度变化时,求异面直线PC与AD所成角的可能范围.
的长度变化时,求异面直线PC与AD所成角的可能范围.
如图,AC是圆O的直径,点B在圆O上, ,
,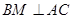 交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,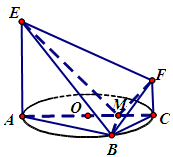
(1)证明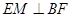 ;
;
(2)(文科)求三棱锥 的体积
的体积
(理科)求平面 和平面
和平面 所成的锐二面角的正切值.
所成的锐二面角的正切值.