（本小题满分10分）关于某设备的使用年限x和所支出的维修费用
（万元），有统计数据
，由资料知对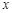
呈线性相关，并且统计的五组数据的平均值分别为
，
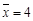，若用五组数据得到的线性回归方程
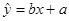去估计，使用8年的维修费用比使用7年的维修费用多1．1万元．
（1）求回归直线方程；
（2）估计使用年限为10年时，维修费用是多少？
（本小题满分12分）直三棱柱
中，
，E，F分别是
的中点，
为棱
上的点．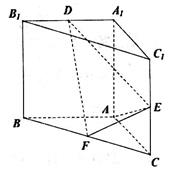
（Ⅰ）证明：
；
（Ⅱ）已知存在一点D，使得平面DEF与平面ABC所成锐二面角的余弦值为
，请说明点D的位置．
（本小题满分12分）在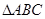
中，边a，b，c的对角分别为A，B，C；且
，面积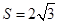
．
（Ⅰ）求a的值；
（Ⅱ）设
，将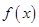
图象上所有点的横坐标变为原来的
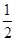（纵坐标不变）得到
的图象，求的单调增区间．
设函数
（其中
）．
（Ⅰ）求函数
的极值；
（Ⅱ）求函数在
上的最小值；
（Ⅲ）若
，判断函数
零点个数．
已知数列
的前
项和为
，
．
（Ⅰ）求数列的通项公式；
（Ⅱ）设数列
的前项和为
,
，点
在直线
上，若存在
，使不等式
成立，求实数
的最大值．
当
且
时，判断
与
的大小，并给出证明．