已知函数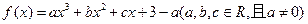 ,当
,当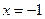 时,
时,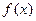 取到极大值2。
取到极大值2。
(1)用关于a的代数式分别表示b和c;
(2)当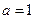 时,求
时,求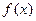 的极小值
的极小值
(3)求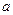 的取值范围。
的取值范围。
(本小题满分12分)
已知数列{ }的前n项和
}的前n项和 =2-
=2- ,数列{
,数列{ }满足b1=1, b3+b7=18,且
}满足b1=1, b3+b7=18,且 +
+ =2
=2 (n≥2).
(n≥2).
(Ⅰ)求数列{ }和{
}和{ }的通项公式;
}的通项公式;
(Ⅱ)若 =
= ,求数列{
,求数列{ }的前n项和
}的前n项和 .
.
((本小题满分14分)
已知函数 是函数
是函数 的极值点。
的极值点。
(Ⅰ)当 时,求a的值,讨论函数
时,求a的值,讨论函数 的单调性;
的单调性;
(Ⅱ)当 R时,函数
R时,函数
 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.
(Ⅲ)是否存在这样的直线 ,同时满足:
,同时满足:
① 是函数
是函数 的图象在点
的图象在点 处的切线
处的切线
②
 与函数
与函数 的图象相切于点
的图象相切于点 ,
,
如果存在,求实数b的取值范围;不存在,请说明理由。
((本小题满分14分)
设数列 为等比数列,数列
为等比数列,数列 满足
满足 ,
, ,已知
,已知 ,
, ,其中
,其中 .
.
(Ⅰ)求数列 的首项和公比;
的首项和公比;
(Ⅱ)当 时,求
时,求 ;
;
(Ⅲ)设 为数列
为数列 的前
的前 项和,若对于任意的正整数
项和,若对于任意的正整数 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
((本小题满分14分)
给定椭圆 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“伴随圆”. 已知椭圆
的“伴随圆”. 已知椭圆 的两个焦点分别是
的两个焦点分别是 ,椭圆
,椭圆 上一动点
上一动点 满足
满足 .
.
(Ⅰ)求椭圆 及其“伴随圆”的方程
及其“伴随圆”的方程
(Ⅱ)试探究y轴上是否存在点 (0,
(0,  )
) ,使得过点
,使得过点 作直线
作直线 与椭圆
与椭圆 只有一个交点,且
只有一个交点,且 截椭圆
截椭圆 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本小题满分12分)
| 日销售量 |
1 |
1.5 |
2 |
| 频数 |
10 |
25 |
15 |
| 频率 |
0.2 |
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
(Ⅰ)填充上表;
(Ⅱ)若以上表频率作为概率,且每天的销售量相互独立.
①5天中该种商品恰好有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元, 表示该种商品两天销售利润的和(单位:
表示该种商品两天销售利润的和(单位:
千元),求 的分布列.
的分布列.