
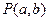

(1) 求实数a、b间满足的等量关系;
(2) 求线段PQ长的最小值;
(3) 若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.
设集合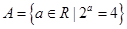 ,
,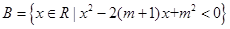 .
.
(1)若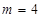 ,求
,求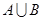 ;
;
(2)若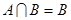 ,求实数
,求实数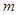 的取值范围.
的取值范围.
已知圆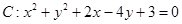 .
.
(1)若圆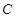 的切线在
的切线在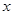 轴和
轴和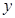 轴上的截距相等,且截距不为零,求此切线的方程;
轴上的截距相等,且截距不为零,求此切线的方程;
(2)从圆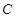 外一点
外一点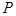 向该圆引一条切线,切点为
向该圆引一条切线,切点为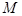 ,
, 为坐标原点,且有
为坐标原点,且有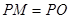 ,求使
,求使 的长取得最小值的点
的长取得最小值的点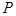 的坐标.
的坐标.
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: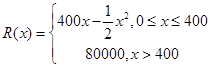 ,其中
,其中 是仪器的月产量.
是仪器的月产量.
(注:总收益=总成本+利润)
(1)将利润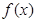 表示为月产量
表示为月产量 的函数;
的函数;
(2)当月产量 为何值时,公司所获利润最大?最大利润为多少元?
为何值时,公司所获利润最大?最大利润为多少元?
已知x0,x0+ 是函数f(x)=cos2
是函数f(x)=cos2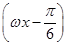 -sin2ωx(ω>0)的两个相邻的零点.
-sin2ωx(ω>0)的两个相邻的零点.
(1)求f 的值;
的值;
(2)若对∀x∈ ,都有|f(x)-m|≤1,求实数m的取值范围.
,都有|f(x)-m|≤1,求实数m的取值范围.
已知向量a=(cos α,sin α),b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),其中0<α<x<π.
(1)若α=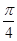 ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;
(2)若a与b的夹角为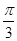 ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值.