(本小题满分12分)某同学用五点法画函数 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
 |
0 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
0 |
5 |
-5 |
0 |
(1)请将上表数据补充完整,并直接写出函数 的解析式;
的解析式;
(2)若函数 的图像向左平移
的图像向左平移 个单位后对应的函数为
个单位后对应的函数为 ,求
,求 的图像离原点最近的对称中心.
的图像离原点最近的对称中心.
(本小题满分12分)已知向量 ,若函数
,若函数
(1)求 的最小正周期;
的最小正周期;
(2)若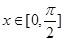 ,求
,求 的单调减区间.
的单调减区间.
(本小题满分10分)已知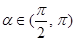 ,且
,且 ,
,
(1)求 的值;
的值;
(2)若 ,
, ,求
,求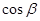 的值.
的值.
(本小题满分12分)设函数 .
.
(1)若函数 在
在 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)①是否存在实数 ,使得关于
,使得关于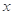 的不等式
的不等式 在
在 上恒成立?若存在,求出
上恒成立?若存在,求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式
(本小题满分12分)
设函数 (
(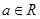 ).
).
(1)当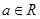 时,讨论函数
时,讨论函数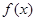 的单调性;
的单调性;
(2)若对任意 及任意
及任意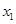 ,
,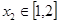 ,恒有
,恒有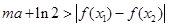 成立,求实数
成立,求实数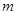 的取值范围.
的取值范围.