如图,在直三棱柱ABC—A1B1C1中,∠ABC=90°,AB=BC=AA1=2,M、N分别是A1C1、BC1的中点.
(I)求证:BC1⊥平面A1B1C;
(II)求证:MN∥平面A1ABB1;
(III)求多面体M—BC1B1的体积.
正四棱锥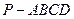 中,
中,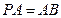 ,
,
点M,N分别在PA,BD上,且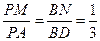 .
.
(Ⅰ)求异面直线MN与AD所成角;
(Ⅱ)求证: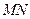 ∥平面PBC;
∥平面PBC;
(Ⅲ)求MN与平面PAB所成角的正弦值.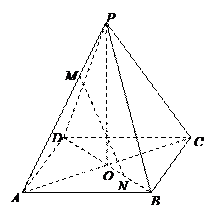
将一枚骰子(形状为正方体,六个面上分别标有数字1,2,3,4,5,6的玩具)先后抛掷两次,骰子向上的点数依次为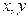 .
.
(1)求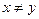 的概率;
的概率;
(2)求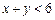 的概率P;
的概率P;
(3)试将右侧求⑵中概率P的伪代码补充完整
已知抛物线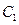 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线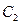 :
: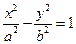 的一个焦点
的一个焦点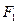 且垂直于
且垂直于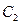 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线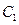 与双曲线
与双曲线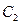 的一个交点是
的一个交点是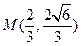 .
.
(1)求抛物线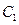 的方程及其焦点
的方程及其焦点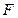 的坐标;
的坐标;
(2)求双曲线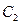 的方程及其离心率
的方程及其离心率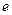 .
.
设p:实数x满足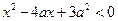 ,其中
,其中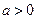 ,命题
,命题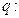 实数
实数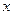 满足
满足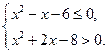 .
.
(Ⅰ)若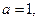 且
且 为真,求实数
为真,求实数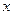 的取值范围;
的取值范围;
(Ⅱ)若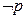 是
是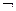
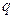 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
设 是一个公差为
是一个公差为
 的等差数列,它的前
的等差数列,它的前
10项和 ,且
,且 成等比数列。
成等比数列。
(1)证明:
(2)求公差 的值和数列
的值和数列 的通项公式。
的通项公式。