已知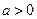 且
且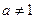 ,
,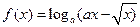 .
.
(1)求函数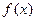 的定义域;
的定义域;
(2)当 时,判断函数
时,判断函数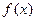 的单调性,并用函数单调性的定义证明你的结论
的单调性,并用函数单调性的定义证明你的结论
(本小题满分14分)已知函数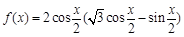 .
.
(1)设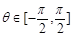 ,且
,且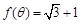 ,求θ的值;
,求θ的值;
(2)在△ABC中,AB=1,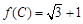 ,且△ABC的面积为
,且△ABC的面积为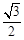 ,求sinA+sinB的值.
,求sinA+sinB的值.
(本小题满分14分)如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2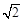 .求证:
.求证:
(1)PA⊥平面EBO;
(2)FG∥平面EBO.
(本小题满分10分)选修4-5:不等式选讲
设函数 ,其中
,其中 .
.
(1)当 时,求不等式
时,求不等式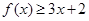 的解集;
的解集;
(2)若不等式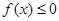 的解集为
的解集为 ,求
,求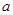 的值.
的值.
(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标的极点在平面直角坐标系的原点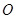 处,极轴与
处,极轴与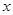 轴的正半轴重合,且长度单位相同。直线
轴的正半轴重合,且长度单位相同。直线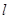 的极坐标方程为:
的极坐标方程为: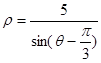 ,点
,点 ,参数
,参数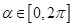 .
.
(1)求点 轨迹的直角坐标方程;
轨迹的直角坐标方程;
(2)求点 到直线
到直线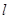 距离的最大值.
距离的最大值.
(本小题满分10分)选修4-1:几何证明选讲
已知 中,
中, ,
, 是
是 外接圆劣弧
外接圆劣弧 上的点(不与点
上的点(不与点 重合),延长
重合),延长 至
至 。
。
(1)求证: 的延长线平分
的延长线平分 ;
;
(2)若 ,
, 中
中 边上的高为
边上的高为 ,求
,求 外接圆的面积。
外接圆的面积。