求过直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点,且到点P(0,4)的距离为1的直线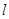 的方程.
的方程.
已知函数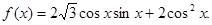
(1)求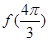 的值;
的值;
(2)当 时,求函数
时,求函数 的值域.
的值域.
已知函数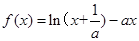 ,其中
,其中 且
且 .
.
(1)讨论 的单调性;
的单调性;
(2) 若不等式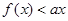 恒成立,求实数
恒成立,求实数 取值范围;
取值范围;
(3)若方程 存在两个异号实根
存在两个异号实根 ,
, ,求证:
,求证:
已知正项数列 中,其前
中,其前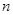 项和为
项和为 ,且
,且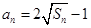 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 是数列
是数列 的前
的前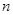 项和,
项和, 是数列
是数列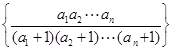 的前
的前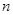 项和,求证:
项和,求证: .
.
已知点 ,
,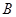 的坐标分别为
的坐标分别为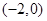 ,
,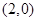 .直线
.直线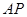 ,
,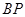 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线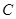 .
.
(1)求曲线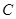 的方程;
的方程;
(2)设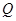 是曲线
是曲线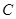 上的动点,直线
上的动点,直线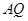 ,
,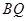 分别交直线
分别交直线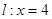 于点
于点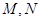 ,线段
,线段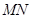 的中点为
的中点为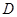 ,求直线
,求直线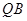 与直线
与直线 的斜率之积的取值范围;
的斜率之积的取值范围;
(3)在(2)的条件下,记直线 与
与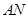 的交点为
的交点为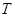 ,试探究点
,试探究点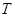 与曲线
与曲线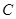 的位置关系,并说明理由.
的位置关系,并说明理由.
如图,正方形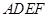 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直,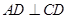 ,
, ∥
∥ ,
,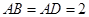 ,
, ,
, 为
为 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 平面
平面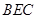 ;
;
(3)求平面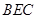 与平面
与平面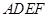 所成锐二面角的余弦值.
所成锐二面角的余弦值.