(本小题满分10分)一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18t;生产1车乙种肥料的主要原料是磷酸盐1t、硝酸盐15t。现库存磷酸盐10t、硝酸盐66t。已知生产1车皮甲种肥料,产生的利润为10000元;生产1车皮乙种肥料,产生的利润为5000元。那么分别生产甲、乙两种肥料各多少车皮,能够产生最大利润?最大利润是多少?
(本小题14分)如图所示,L是海面上一条南北方向的海防警戒线,在L上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1. 5 km/s.
(1)设A到P的距离为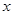 km,用
km,用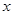 分别表示B、C到P 的距离,并求
分别表示B、C到P 的距离,并求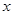 值;
值;
(2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)。 
.(本小题14分)在等差数列 中,
中, ,前
,前 项和
项和 满足条件
满足条件 ,
,
(1)求数列 的通项公式和
的通项公式和 ;
;
(2)记 ,求数列
,求数列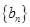 的前
的前 项和
项和

(本小题14分)某工厂要制造A种电子装置41台,B种电子装置66台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2㎡,可做A、B的外壳分别为2个和7个,乙种薄钢板每张面积5㎡,可做A、B的外壳分别为7个和9个,求两种薄钢板各用多少张,才能使总的用料面积最小?
(本小题13分)某工厂要建造一个无盖长方体水池,底面一边长固定为8 ,最大装水量为72
,最大装水量为72 ,池底和池壁的造价分别为
,池底和池壁的造价分别为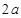 元
元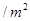 、
、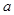 元
元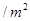 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?