(本小题满分10分)一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t,硝酸盐18t;生产1车乙种肥料的主要原料是磷酸盐1t、硝酸盐15t。现库存磷酸盐10t、硝酸盐66t。已知生产1车皮甲种肥料,产生的利润为10000元;生产1车皮乙种肥料,产生的利润为5000元。那么分别生产甲、乙两种肥料各多少车皮,能够产生最大利润?最大利润是多少?
(本小题满分14分)
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),α∈(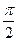 ,
, )。
)。
(1)若|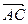 |=|
|=| |,求角α的值;
|,求角α的值;
(2)若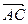 ·
·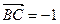 ,求
,求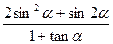 的值
的值
本小题满分12分)
已知函数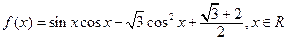
(1)求函数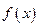 的最小正周期及函数取最小值时自变量
的最小正周期及函数取最小值时自变量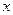 的集合
的集合
(2)确定函数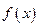 的单调递增区间
的单调递增区间
(3)若函数y=sin2x的图象向右平移m个单位(|m|<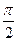 ),向上平移n个单位后得到函数y=f(x)的图象,求实数m、n的值
),向上平移n个单位后得到函数y=f(x)的图象,求实数m、n的值
(本小题满分10分)
已知向量: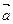 =(cos
=(cos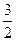 x,sin
x,sin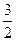 x),
x),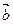 =(cos
=(cos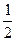 x,-sin
x,-sin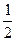 x),且x∈[
x),且x∈[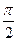 ,π]
,π]
(1)求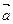 ·
·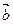 ,|
,|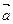 +
+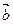 |
|
(2)求f(x)=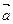 ·
·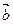 +2|
+2|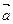 +
+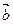 |的最小值
|的最小值
(本小题满分8分)
如图,在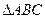 中,D、E分别是AB、AC的中点,DM=
中,D、E分别是AB、AC的中点,DM=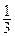 DE,若
DE,若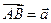 ,
,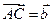
(1)用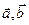 表示
表示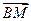
(2)若N为线段BC上的点,且BN=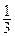 BC,用向量方法证明:A、M、N三点共线
BC,用向量方法证明:A、M、N三点共线
(本小题满分10分
已知 =(1,2),
=(1,2),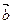 =(x,1),分别求x的值使
=(x,1),分别求x的值使
①(2 +
+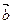 )⊥(
)⊥( -2
-2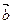 );②(2
);②(2 +
+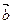 )∥(
)∥( -2
-2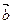 );③
);③ 与
与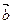 的夹角是600
的夹角是600