(本小题满分12分)
雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示。
| |
男 |
女 |
| 文科 |
2 |
5 |
| 理科 |
10 |
3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据:
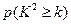 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
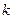 |
2.07 |
2.71 |
3.84 |
5.02 |
6.64 |
7.88 |
10.83 |
已知函数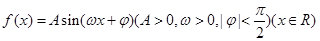 的部分图象如图所示.
的部分图象如图所示.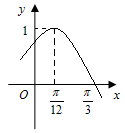
(1)求 的表达式;
的表达式;
(2)设 ,求函数
,求函数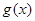 的最小值及相应的
的最小值及相应的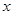 的取值集合.
的取值集合.
已知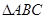 内角
内角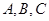 所对边长分别为
所对边长分别为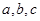 ,面积
,面积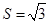 ,且
,且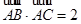 .
.
(1)求角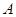 ;
;
(2)若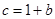 ,求
,求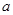 的值.
的值.
已知函数 ,
, 为
为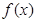 的导函数。(1)求函数
的导函数。(1)求函数 的单调递减区间;
的单调递减区间;
(2)若对一切的实数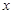 ,有
,有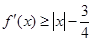 成立,求
成立,求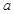 的取值范围;
的取值范围;
(3)当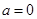 时,在曲线
时,在曲线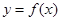 上是否存在两点
上是否存在两点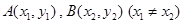 ,使得曲线在
,使得曲线在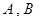 两点处的切线均与直线
两点处的切线均与直线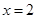 交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
已知 为椭圆
为椭圆 :
: 的左、右焦点,过椭圆右焦点F2斜率为
的左、右焦点,过椭圆右焦点F2斜率为 (
( )的直线
)的直线 与椭圆
与椭圆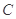 相交于
相交于 两点,
两点, 的周长为8,且椭圆C与圆
的周长为8,且椭圆C与圆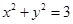 相切。
相切。
(1)求椭圆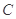 的方程;
的方程;
(2)设 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线 于点
于点 ,线段
,线段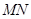 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 ,求证
,求证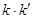 为定值.
为定值.
如图,在四棱锥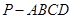 中,
中, 为
为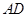 上一点,面
上一点,面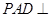 面
面 ,四边形
,四边形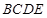 为矩形
为矩形 ,
, ,
,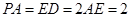 .
.
(1)已知 ,且
,且 ∥面
∥面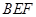 ,求
,求 的值;
的值;
(2)求证: 面
面 ,并求点
,并求点 到面
到面 的距离.
的距离.