已知数列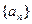 满足条件:
满足条件: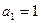 ,
,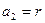 (
(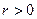 ),且
),且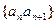 是公比为q (
是公比为q (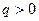 )的等比数列.设
)的等比数列.设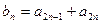 (
(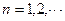 ),求
),求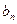 与
与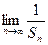 ,其中
,其中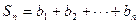
(本小题满分12分)
已知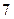 件产品中有
件产品中有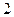 件次品,现逐一不放回地进行检验,直到
件次品,现逐一不放回地进行检验,直到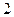 件次品都能被确认为止(如:前
件次品都能被确认为止(如:前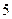 次检验到的产品均不为次品,则次品也被确认).
次检验到的产品均不为次品,则次品也被确认).
(Ⅰ)求检验次数为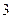 的概率;
的概率;
(Ⅱ)求检验次数为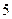 的概率.
的概率.
(本小题满分10分)
已知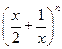 各项展开式的二项式系数之和为
各项展开式的二项式系数之和为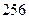 .
.
(Ⅰ)求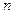 ;(Ⅱ)求展开式中的常数项.
;(Ⅱ)求展开式中的常数项.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题 满分8分.
满分8分.
从数列 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 的一个子数列.
的一个子数列.
设数列 是一个首项为
是一个首项为 、公差为
、公差为
 的无穷等差数列.
的无穷等差数列.
(1)若 ,
, ,
, 成等
成等 比数列,求其公比
比数列,求其公比 .
.
(2)若 ,从数列
,从数列 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若 ,从数列
,从数列 中取出第1项、第
中取出第1项、第
 项(设
项(设 )作为一个等比数列的第1项、第2项,试问当且仅当
)作为一个等比数列的第1项、第2项,试问当且仅当 为何值时,该数列为
为何值时,该数列为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知椭圆 :
: (
( ),其焦距为
),其焦距为 ,若
,若 (
( ),则称椭圆
),则称椭圆 为“黄金椭圆”.
为“黄金椭圆”.
(1)求证:在黄金椭圆 :
: (
( )中,
)中, 、
、 、
、 成等比数列.
成等比数列.
(2)黄金椭圆 :
: (
( )的右焦点为
)的右焦点为 ,
, 为椭圆
为椭圆 上的
上的
任意一点.是否存在过点 、
、 的直线
的直线 ,使
,使 与
与 轴的交点
轴的交点 满足
满足 ?若存在,求直线
?若存在,求直线 的斜率
的斜率 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)在黄金椭圆中有真命题:已知黄金椭圆 :
: (
( )的左、右
)的左、右
焦点分别是 、
、 ,以
,以 、
、 、
、 、
、 为顶点的菱形
为顶点的菱形 的内切圆过焦点
的内切圆过焦点 、
、 .
.
试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
本题共有2个小题,第1小题满分8分,第2小题满分8分.
如图,反比例函数 (
( )的图像过点
)的图像过点 和
和 ,点
,点 为该函数图像上一动点,过
为该函数图像上一动点,过 分别作
分别作 轴、
轴、 轴的垂线,垂足为
轴的垂线,垂足为 、
、 .记四边形
.记四边形 (
( 为坐标原点)与三角形
为坐标原点)与三角形 的公共部分面积为
的公共部分面积为 .
.
(1)求 关于
关于 的表达式;
的表达式;
(2)求 的最大值及此时
的最大值及此时 的值.
的值.