(本小题10分)设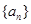 是由正数组成的等比数列,
是由正数组成的等比数列, 是其前n项和,
是其前n项和,
证明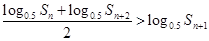 。
。
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=A,AB=2,以AC的中点O为球心、AC为直径的球面交PD于点M。
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成的角的大小;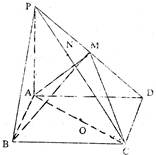
已知△ABC的面积S满足
(Ⅰ)求θ的取值范围;
(Ⅱ)求函数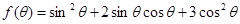 的最大值。
的最大值。
.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P—EFGH,下半部分是长方体ABCD—EFGH,图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线BD⊥平面PEG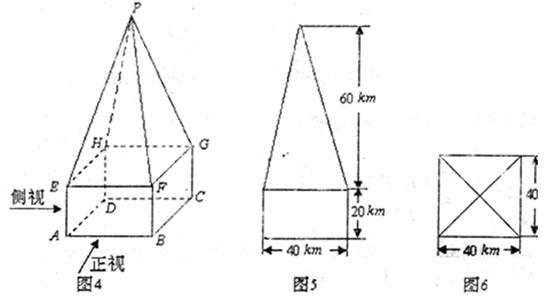
.已知函数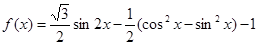
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对边分别为a,b,c,且c=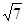 ,
,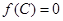 ,若向量
,若向量 共线,求a , b的值。
共线,求a , b的值。
(本小题满分l2分)(注意:在试题卷上作答无效)
已知函数f(x)=x3+bx2+ax+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.