(本小题满分14分)
已知数列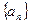 中,
中,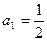 ,点
,点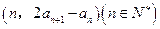 在直线
在直线 上.
上.
(Ⅰ)计算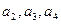 的值;
的值;
(Ⅱ)令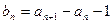 ,求证:数列
,求证:数列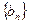 是等比数列;
是等比数列;
(Ⅲ)求数列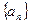 的通项公式.
的通项公式.
(本小题满分12分)已知向量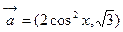 ,
,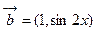 ,函数
,函数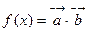 ,
,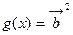 .
.
(1)求函数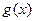 的最小正周期;
的最小正周期;
(2)在
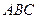 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
,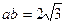 ,且
,且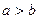 ,求
,求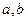 的值.
的值.
(本题满分12分) 已知直线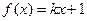 (
( ),若点(
),若点(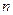 ,
,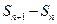 )
)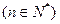 在
在
此直线上,并有 ,
, (
(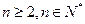 ).
).
(1)求直线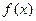 的斜率
的斜率 的值;
的值;
(2)若 是数列
是数列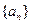 的前
的前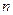 项和,求
项和,求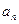 的通项公式.
的通项公式.
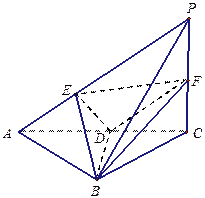
(本题满分10分) 已知三棱锥P—ABC中,PC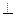 底面ABC,AB=BC,D、F分别为
底面ABC,AB=BC,D、F分别为
AC、PC的中点,DE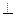 AP于E。
AP于E。
(1)求证:AP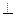 平面BDE;
平面BDE;
(2)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
 |
(本题满分10分) 如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它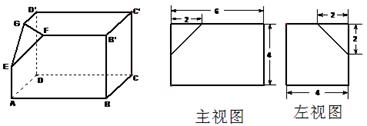
的主视图和左视图在右面画出(单位:cm).
(1)按照给出的尺寸,求该多面体的体积;
(2)在所给直观图中连结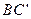 ,证明:
,证明: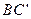 ∥面EFG。
∥面EFG。
(本题满分10分)已知圆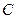 过点
过点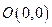 ,
,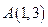 ,
,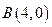 .
.
(1)求圆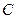 的方程;
的方程;
(2)若直线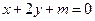 与圆
与圆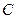 相交于
相交于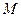 、
、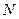 两点,且
两点,且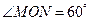 ,求
,求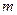 的值.
的值.