有道解三形的题目,因纸张破损致使有一个条件不清,具体如下:在 中,已知
中,已知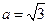 ,
, , ,求角A。经推断,破损处的条件为三角形一边的长度,且答案提示解
, ,求角A。经推断,破损处的条件为三角形一边的长度,且答案提示解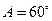 ,试将条件补充完整,并说明理由。
,试将条件补充完整,并说明理由。
已知正项数列{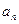 }的前n项和为
}的前n项和为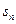 对任意
对任意 ,
,
都有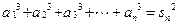 。(Ⅰ)求数列
。(Ⅰ)求数列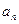 的通项公式;
的通项公式;
(Ⅱ)若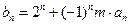 是递增数列,求实数m的取值范围。
是递增数列,求实数m的取值范围。
在五棱锥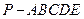 中,PA=AB=AE=2
中,PA=AB=AE=2 ,PB=PE=
,PB=PE=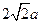 , BC=DE=
, BC=DE= ,
,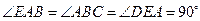 .(Ⅰ)求证:PA
.(Ⅰ)求证:PA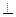 平面
平面 (Ⅱ)求二面角
(Ⅱ)求二面角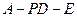 的大小。
的大小。
袋中装有大小相同的10个球,其中5个白球,3个红球,2个黑球,现在依次从中取出3个球。(Ⅰ)求取出的3个球不是同一种颜色的概率;(Ⅱ)求取出的3个球中所含红球的个数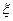 的分布列及期望。
的分布列及期望。
已知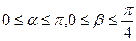 ,且
,且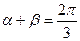 .
.
求: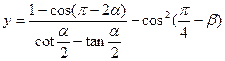 的最大值,并求出相应的
的最大值,并求出相应的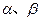 的值.
的值.