(CUA)∪B, A∩(CUB).
选修4—1:几何证明选讲
已知AB是圆O的直径,P是上半圆上的任意一点,PC是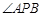 的平分线,
的平分线,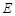 是下半圆的中点.
是下半圆的中点.
求证:直线PC经过点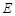 .
.
(本小题满分16分)已知 为实数,函数
为实数,函数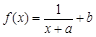 ,函数
,函数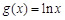 .
.
(1)当 时,令
时,令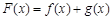 ,求函数
,求函数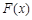 的极值;
的极值;
(2)当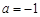 时,令
时,令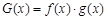 ,是否存在实数
,是否存在实数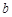 ,使得对于函数
,使得对于函数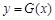 定义域中的任意实数
定义域中的任意实数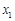 ,均存在实数
,均存在实数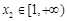 ,有
,有 成立,若存在,求出实数
成立,若存在,求出实数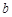 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
(本小题满分16分)
在数列 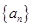 中,已知
中,已知 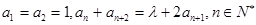 ,
,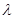 为常数.
为常数.
(1)证明: 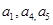 成等差数列;
成等差数列;
(2)设  ,求数列 的前n项和
,求数列 的前n项和 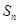 ;
;
(3)当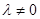 时,数列
时,数列 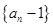 中是否存在三项
中是否存在三项 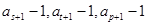 成等比数列,且
成等比数列,且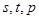 也成等比数列?若存在,求出
也成等比数列?若存在,求出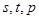 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【原创】已知椭圆 ,椭圆
,椭圆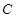 过点
过点 且与抛物线
且与抛物线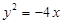 有一个公共的焦点.
有一个公共的焦点.
(1)求椭圆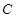 方程;
方程;
(2)若点 在椭圆
在椭圆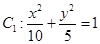 上,点
上,点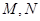 在椭圆
在椭圆 上,且满足
上,且满足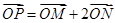 ,则直线
,则直线 与直线
与直线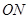 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
(本小题满分16分)如图,有一个长方形地块ABCD,边AB为2km, AD为4 km.,地块的一角是湿地(图中阴影部分),其边缘线AC是以直线AD为对称轴,以A为顶点的抛物线的一部分.现要铺设一条过边缘线AC上一点P的直线型隔离带EF,E,F分别在边AB,BC上(隔离带不能穿越湿地,且占地面积忽略不计).设点P到边AD的距离为t(单位:km),△BEF的面积为S(单位:  ).
).
(1)求S关于t的函数解析式,并指出该函数的定义域;
(2)是否存在点P,使隔离出的△BEF面积S超过3  ?并说明理由.
?并说明理由.