(1)解不等式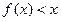 ;
;
(2)如果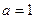 ,且
,且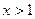 ,求
,求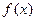 的取值范围
的取值范围
已知函数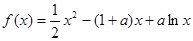 ,其中
,其中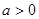 .
.
(Ⅰ) 求函数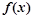 的极小值点;
的极小值点;
(Ⅱ)若曲线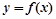 在点
在点 处的切线都与
处的切线都与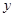 轴垂直,问是否存在常数
轴垂直,问是否存在常数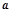 ,使函数
,使函数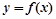 在区间
在区间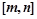 上存在零点?如果存在,求
上存在零点?如果存在,求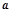 的值:如果不存在,请说明理由.
的值:如果不存在,请说明理由.
平面内与两定点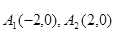 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数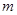 的点的轨迹,加上
的点的轨迹,加上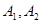 两点,所成的曲线
两点,所成的曲线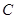 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(I)求曲线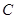 的方程,并讨论
的方程,并讨论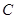 的形状与
的形状与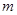 值的关系.
值的关系.
(Ⅱ)当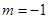 时,对应的曲线为
时,对应的曲线为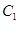 ;对给定的
;对给定的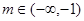 ,对应的曲线为
,对应的曲线为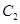 ,若曲线
,若曲线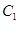 的斜率为
的斜率为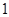 的切线与曲线
的切线与曲线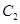 相交于
相交于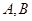 两点,且
两点,且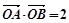 (
(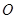 为坐标原点),求曲线
为坐标原点),求曲线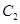 的方程.
的方程.
城市的空气质量以其空气质量指数API(为整数)衡量,指数越大,级别越高,说明污染越严重,对人体健康的影响也越明显.根据空气质量指数API的不同,可将空气质量分级如下表:
| API |
0~50 |
51~100 |
101~150 |
151~200 |
201~250 |
251~300 |
>300 |
| 状况 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中度重污染 |
重度污染 |
为了了解某城市2011年的空气质量情况,现从该城市一年空气质量指数API的监测数据库中,用简单随机抽样方法抽取30个空气质量指数API进行分析,得到如下数据:
| API分组 |
 |
 |
 |
 |
 |
 |
 |
| 频数 |
2 |
1 |
4 |
6 |
10 |
5 |
2 |

(Ⅰ)完成下面频率分布直方图,并求质量指数API的中位数大小;
(Ⅱ)估计该城市一年中空气质量为优良的概率;
(Ⅲ)请你依据所给数据和上述分级标准,对该城市的空气质量给出一个简短评价.
如图,四棱锥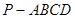 的底面为矩形,
的底面为矩形,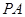 是四棱锥的高,
是四棱锥的高,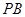 与
与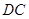 所成角为
所成角为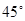 ,
, 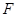 是
是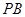 的中点,
的中点,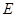 是
是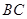 上的动点.
上的动点.
(Ⅰ)证明: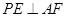 ;
;
(Ⅱ)若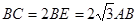 ,求直线
,求直线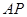 与平面
与平面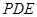 所成角的大小.
所成角的大小.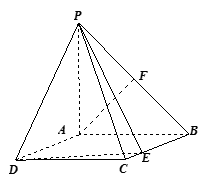
在 中,
中,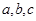 分别为内角
分别为内角 所对的边,且满足
所对的边,且满足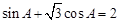 .
.
(Ⅰ)求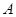 的大小;
的大小;
(Ⅱ)现给出三个条件:①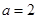 ; ②
; ② ;③
;③ .
.
试从中选出两个可以确定 的条件,写出你的选择并以此为依据求
的条件,写出你的选择并以此为依据求 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)