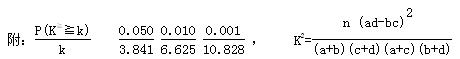以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线 的参数方程为
的参数方程为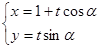 (t为参数,0<a<
(t为参数,0<a< ),曲线C的极坐标方程为
),曲线C的极坐标方程为 .
.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A、B两点,当a变化时,求|AB|的最小值.
(本小题满分12分)
已知一四棱锥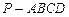 的底面是边长为1的正方形,侧棱
的底面是边长为1的正方形,侧棱 底面
底面 ,且
,且 .
.
(1)求证: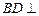 平面
平面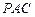
(2)若点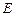 为
为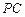 的中点,求二面角
的中点,求二面角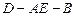 的大小.
的大小.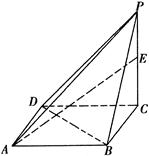
(本小题满分10分)
某地区为下岗女职工免费提供财会和家政培训,以提高下岗女职工的再就业能力,每名下岗人员可以参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有50%,参加过家政培训的有80%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响
(1)任选1名下岗女职工,求该人参加过培训的概率
(2)任选3名下岗女职工,记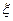 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求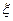 的分布列和期望
的分布列和期望
(本小题满分12分)
已知向量 ,且A、B、C分别为
,且A、B、C分别为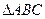 的三边a、b、c所对的角。
的三边a、b、c所对的角。
(1)求角C的大小;
(2)若三边a,c,b成等差数列,且 求c边的长。
求c边的长。
(本小题满分12分)在 ABC中,C-A=
ABC中,C-A= , sinB=
, sinB=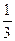
(I)求sinA的值
(II)设AC= ,求△ABC的面积。
,求△ABC的面积。
(本小题满分12分) 某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂:
| 分组 |
 |
 |
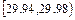 |
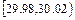 |
 |
 |
 |
| 频数 |
12 |
63 |
86 |
182 |
92 |
61 |
4 |
乙厂:
| 分组 |
 |
 |
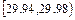 |
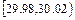 |
 |
 |
 |
| 频数 |
29 |
71 |
85 |
159 |
76 |
62 |
18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填入答题卡的 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。