如图所示，平行六面体ABCD—A1B1C1D1中，以顶点A为端点的三条棱长都为1，且两两夹角为60°．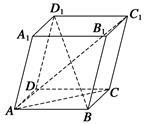
（1）求AC1的长；
（2）求BD1与AC夹角的余弦值．
设数列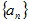
的前n项和为
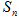，且满足
．
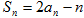（1）求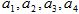
；
（2）猜想数列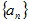的通项公式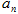
，并用数学归纳法证明
（本小题满分10分）已知函数f（x）＝ax3＋cx＋d（a≠0）是R上的奇函数，当x＝1时，f（x）取得极值－2．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调区间和极大值；
（本小题满分12分）已知函数
．
（Ⅰ）求函数
的单调递增区间；
（Ⅱ）证明：当
时，
；
（Ⅲ）确定实数
的所有可能取值，使得存在
，当
时，恒有
．
（本小题满分12分）已知函数
（Ⅰ）讨论函数
的单调性；
（Ⅱ）证明：若
，则对任意
，
，有
．
，直线
。
，直线
与圆C总有两个不同交点.