如图,已知平面内一动点 到两个定点
到两个定点 、
、 的距离之和为
的距离之和为 ,线段
,线段 的长为
的长为 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 作直线
作直线 与轨迹
与轨迹 交于
交于 、
、 两点,且点
两点,且点 在线段
在线段 的上方,
的上方,
线段 的垂直平分线为
的垂直平分线为 .
.
①求 的面积的最大值;
的面积的最大值;
②轨迹 上是否存在除
上是否存在除 、
、 外的两点
外的两点 、
、 关于直线
关于直线 对称,请说明理由.
对称,请说明理由.
(本小题满分12分)双曲线C与椭圆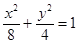 有相同的焦点,直线y=
有相同的焦点,直线y=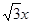 为
为 的一条渐近线.
的一条渐近线.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)过点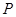 (0,4)的直线
(0,4)的直线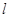 ,交双曲线
,交双曲线 于A,B两点,交x轴于
于A,B两点,交x轴于 点(
点( 点与
点与 的顶点不重合)。当
的顶点不重合)。当 =
=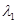
 ,且
,且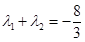 时,求
时,求 点的坐标
点的坐标
(本小题满分12分)设等比数列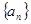 的公比为
的公比为 ,前n项和
,前n项和 。
。
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)设 ,记
,记 的前n项和为
的前n项和为 ,试比较
,试比较 与
与 的大小。
的大小。
(本小题满分12分)右图是一个直三棱柱(以 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为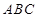 已知
已知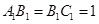 ,
, ,
, ,
, ,
,

(Ⅰ)设点 是
是 的中点,证明:
的中点,证明: 平面
平面 ;
;
(Ⅱ)求二面角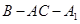 的大小;
的大小;
(本小题满分12分)袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)计分介于20分到40分之间的概率
(本小题满分10分)在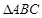 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 ,已知向量
,已知向量 ,
, ,且
,且 。
。
(Ⅰ)求角A的大小;
(Ⅱ)若 ,求
,求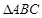 面积的最大值。
面积的最大值。