已知函数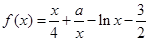 ,其中a∈R,且曲线
,其中a∈R,且曲线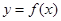 在点
在点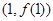 处的切线垂直于直线
处的切线垂直于直线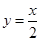 .
.
(1)求a的值;
(2)求函数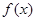 的单调区间.
的单调区间.
已知函数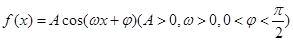 的图象过点(0,
的图象过点(0,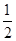 ),最小正周期为
),最小正周期为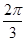 ,且最小值为-1.
,且最小值为-1.
(1)求函数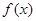 的解析式.
的解析式.
(2)若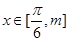 ,
,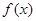 的值域是
的值域是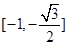 ,求m的取值范围.
,求m的取值范围.
等差数列{an}的前n项和为Sn,已知S3=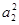 ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,
(1)求数列{an}的通项公式.
(2)若{an}又是等比数列,令bn=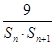 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
已知函数
,
.
(Ⅰ)当
时,求不等式
的解集;
(Ⅱ)设
,且当
时,
,求
的取值范围。
已知曲线
的参数方程为
(
为参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
.
(1)把
的参数方程化为极坐标方程;
(2)求
与
交点的极坐标(
).
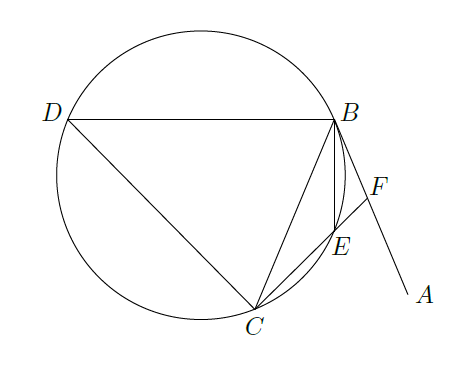
如图,直线
为圆的切线,切点为
,点
在圆上,
的角平分线
交圆于点
,
垂直
交圆于点
。
(Ⅰ)证明:
;
(Ⅱ)设圆的半径为
,
,延长
交
于点
,求
外接圆的半径。