等差数列{an}的前n项和为Sn,已知S3=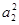 ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,
(1)求数列{an}的通项公式.
(2)若{an}又是等比数列,令bn=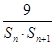 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
在△ABC中,角A、B、C的对边分别为a、b、c,且满足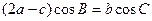 .
.
(Ⅰ)求角B的大小;
(Ⅱ)设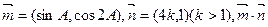 的最大值为5,求k的值.
的最大值为5,求k的值.
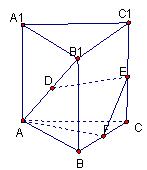
如图,已知直三棱柱 中,
中,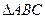 为等腰直角三角形,
为等腰直角三角形,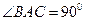 ,且
,且 ,
,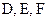 分别为
分别为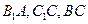 的中点。
的中点。
(Ⅰ)求证: //平面
//平面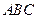 ;
;
(Ⅱ)求证: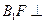 平面
平面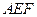 ;
;
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率.
设函数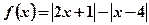 。(1)求不等式
。(1)求不等式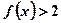 的解集;(2)求函数
的解集;(2)求函数 的最小值
的最小值
已知直线的极坐标方程为 ,圆
,圆 的参数方程为
的参数方程为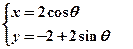 (其中
(其中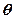 为参数)
为参数)
(1)将直线的极坐标方程化为直角坐标方程;(2)求圆 上的点到直线的距离的最小值
上的点到直线的距离的最小值