已知椭圆E: 过点D(1,
过点D(1, ),且右焦点为F(1,0),右顶点为A.过点F的弦为BC.直线BA,直线CA分别交直线l:x=m,(m>2)于P、Q两点.
),且右焦点为F(1,0),右顶点为A.过点F的弦为BC.直线BA,直线CA分别交直线l:x=m,(m>2)于P、Q两点.
(1)求椭圆方程;
(2)若FP⊥FQ,求m的值.
如图,相距14km的两个居民小区M和N位于河岸l(直线)的同侧,M和N距离河岸分别为10km和8km.现要在河的小区一侧选一地点P,在P处建一个生活污水处理站,从P排直线水管PM,PN分别到两个小区和垂直于河岸的水管PQ,使小区污水经处理后排入河道.设PQ段长为t km(0 < t < 8).
(1)求污水处理站P到两小区的水管的总长最小值(用t表示);
(2)请确定污水处理站P的位置,使所排三段水管的总长最小,并求出此时污水处理站分别到两小区水管的长度.
已知直三棱柱 中,
中, 分别为
分别为 的中点,
的中点, ,点
,点 在线段
在线段 上,且
上,且 .
.
(1)证: ;
;
(2)若 为线段
为线段 上一点,试确定
上一点,试确定 在线段
在线段 上的位置,使得
上的位置,使得 平面
平面 .
.
在△ABC中, 分别为角A、B、C的对边,若
分别为角A、B、C的对边,若 =(
=( ,
, ),
),  ,且
,且
 .
.
(1)求角A的度数;
(2)当 ,且△ABC的面积
,且△ABC的面积 时,求边
时,求边 的值和△ABC的面积。
的值和△ABC的面积。
已知圆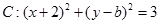
 过点
过点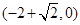 , 直线
, 直线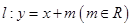 .
.
(1)求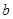 的值;
的值;
(2)若直线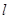 与圆C相切,求
与圆C相切,求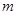 的值;
的值;
(3)若直线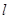 与圆C相交于M、N两点,且
与圆C相交于M、N两点,且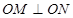 (O为原点),求实数
(O为原点),求实数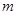 的值.
的值.