在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相邻整数的概率;
(Ⅱ)求取出的两个球上标号之和能被3整除的概率.
(本小题满分为12分)
已知函数 .
.
(Ⅰ)求 的最小正周期;(Ⅱ)求
的最小正周期;(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
已知向量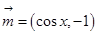 ,向量
,向量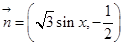 ,函数
,函数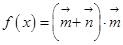 .
.
(Ⅰ)求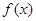 的最小正周期
的最小正周期 ;
;
(Ⅱ)已知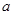 ,
,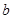 ,
,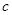 分别为
分别为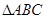 内角
内角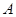 ,
,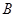 ,
,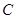 的对边,
的对边,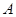 为锐角,
为锐角,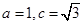 ,且
,且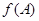
恰是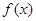 在
在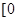 ,
, 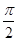
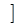 上的最大值,求
上的最大值,求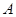 ,
,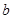 和
和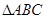 的面积.
的面积.
(本小题满分14分)
已知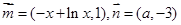
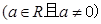 , 函数
, 函数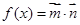 .
.
(Ⅰ)求函数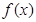 的单调区间;
的单调区间;
(Ⅱ)若函数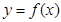 的图像在点
的图像在点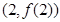 处的切线的斜率为
处的切线的斜率为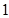 ,问:
,问: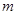 在什么范围
在什么范围
取值时,对于任意的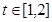 ,函数
,函数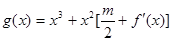 在区间
在区间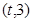 上总存在
上总存在
极值?
(Ⅲ)当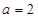 时,设函数
时,设函数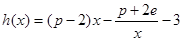 ,若在区间
,若在区间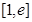 上至少存在
上至少存在
一个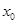 ,使得
,使得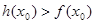 成立,试求实数
成立,试求实数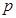 的取值范围.
的取值范围.
(本小题满分12分)
给定椭圆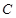 :
: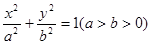 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为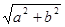 的圆是
的圆是
椭圆 的“准圆”。若椭圆
的“准圆”。若椭圆 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到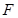 的距
的距
离为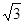 .
.
(Ⅰ)求椭圆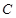 的方程和其“准圆”方程.
的方程和其“准圆”方程.
(Ⅱ)点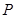 是椭圆
是椭圆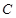 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点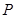 作直线
作直线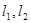 使得
使得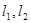 与椭
与椭
圆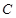 都只有一个交点,且
都只有一个交点,且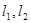 分别交其“准圆”于点
分别交其“准圆”于点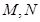 ;
;
(1)当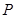 为“准圆”与
为“准圆”与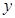 轴正半轴的交点时,求
轴正半轴的交点时,求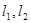 的方程.
的方程.
(2)求证: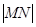 为定值.
为定值.
(本小题满分12分)
已知单调递增的等比数列{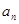 }满足:
}满足: ,且
,且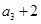 是
是 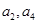 的等差中
的等差中
项.(1)求数列{an}的通项公式.
(2)若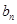 =
=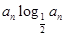 ,sn为数列
,sn为数列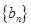 的前
的前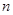 项和,求证:sn
项和,求证:sn
 .
.