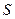已知曲线
的参数方程为
(
为参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
.
(1)把
的参数方程化为极坐标方程;
(2)求
与
交点的极坐标(
).
已知函数f (x) = x3 -(l-3)x2 -(l +3)x + l-1(l > 0)在区间[n, m]上为减函数,记m的最大值为m0,n的最小值为n0,且满足m0-n0 = 4.
 (1)求m0,n0的值以及函数f (x)的解析式;
(1)求m0,n0的值以及函数f (x)的解析式;
(2)已知等差数列{xn}的首项 .又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
.又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
(3)若对任意x1,x2∈[a, m0](x1≠x2),都有 成立,求a的最小值.
成立,求a的最小值.
 BCD.
BCD.
(1)问BC边上是否存在点Q,使得PQ⊥QD,并说明理由
(2)若PA=1,且BC边上有且只有一个点Q,使得PQ⊥QD,求此时二面角Q—PD—A的正切值.



 .
.
(Ⅰ)求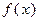 的解析式;
的解析式;
(Ⅱ)若数列 满足:
满足: (
(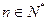 ),且
),且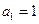 ,求数列
,求数列 的通项;
的通项;
(Ⅲ)求证: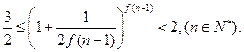
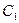

(1)求动圆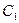 圆心的轨迹C;
圆心的轨迹C;
(2)过点T(-2,0)作直线l与轨迹C交于A、B两点,求一点 ,使得
,使得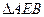 是以点E为直角顶点的等腰直角三角形。
是以点E为直角顶点的等腰直角三角形。
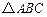

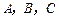

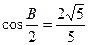
(1)求角B的余弦值;
(2)求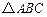 的面积
的面积