求证:(1)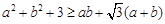 ;
;
(2)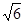 +
+ >2
>2 +
+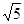 .
.
已知椭圆 的方程为:
的方程为: ,其焦点在
,其焦点在 轴上,离心率
轴上,离心率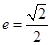 .
.
(1)求该椭圆的标准方程;
(2)设动点 满足
满足 ,其
,其 中M,N是椭圆
中M,N是椭圆 上的点,直线OM与ON的斜率之积为
上的点,直线OM与ON的斜率之积为 ,求证:
,求证: 为定值.
为定值.
(3)在(2)的条件下,问:是否存在两个定点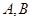 ,使得
,使得 为定值?
为定值?
若存在 ,给出证明;若不存在,请说明理由.
,给出证明;若不存在,请说明理由.
如图,四棱锥 的底面是正方形,
的底面是正方形, ⊥平面
⊥平面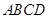 ,
, ,点E是SD上的点,且
,点E是SD上的点,且 .
.
(1)求证:对任意的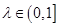 ,都有AC⊥BE;
,都有AC⊥BE;
(2)若二面角C-AE-D的大小为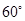 ,求
,求 的值
的值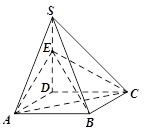
设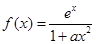 ,其中
,其中 为正实数.
为正实数.
(1)当 时,求
时,求 的极值点;
的极值点;
(2)若 为
为 上的单调函数,求
上的单调函数,求 的取值范围.
的取值范围.
如图,渔船甲位于岛屿 的南偏西
的南偏西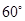 方向的
方向的 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正
出发沿正 北方向航行,若渔船甲同时从
北方向航行,若渔船甲同时从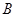 处出发沿北偏东
处出发沿北偏东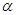 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度;
(2)求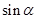 的值.
的值.
设椭圆C1: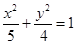 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点)。如图,若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点)。如图,若抛物线C2: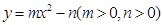 与y轴的交点为B,且经过F1,F2两点。
与y轴的交点为B,且经过F1,F2两点。
1.求抛物线C2的方程;
2.设M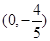 ,N为抛物线C2上的动点,过点N作抛物线C2的切线交椭圆C1于点P、Q两点,求△MPQ面积的最大值。
,N为抛物线C2上的动点,过点N作抛物线C2的切线交椭圆C1于点P、Q两点,求△MPQ面积的最大值。